Professor Diminoi
EXAME NACIONAL DO ENSINO MÉDIO
PROVA DE CIÊNCIAS DA NATUREZA E SUAS TECNOLOGIAS
PROVA DE MATEMÁTICA E SUAS TECNOLOGIAS – PROVA AMARELA – 2º DIA
QUESTÃO 91
O esquema representa um experimento feito com células do protozoário Amoeba proteus. Nele, um grupo de células foi tratado com a droga citocalasina B, enquanto outro grupo não foi tratado, servindo como controle. O formato e o movimento das células tratadas foram comprometidos.
SADAVA, D. et al. Vida: a ciência da biologia - volume I: célula e hereditariedade.
Porto Alegre: Artmed, 2009 (adaptado).
Qual componente celular foi afetado pela droga utilizada no experimento?
(A) Vacúolos.
(B) Mitocôndrias.
(C) Microfilamentos.
(D) Material genético.
(E) Membrana plasmática.
Resolução:
A citocalasina B afetou os microfilamentos, componentes do citoesqueleto que são responsáveis pela emissão dos pseudópodes, expansões da membrana que promovem o movimento ameboide.
Alternativa: C
QUESTÃO 92
O magnésio metálico utilizado em ligas leves é produzido em um processo que envolve várias etapas e utiliza água do mar como matéria-prima. A primeira etapa desse processo consiste na reação entre o íon Mg to the power of 2 plus end exponent e hidróxido de cálcio, Ca open parentheses OH close parentheses subscript 2, obtendo uma mistura que contém hidróxido de magnésio, pouco solúvel, e íons Ca to the power of 2 plus end exponent, de acordo com a equação química:
O método adequado para separar o Mg (OH2(s) dessa mistura é a
(A) filtração.
(B) catação.
(C) destilação.
(D) dissolução.
(E) evaporação.
Resolução:
Filtração é um método de separação que pode isolar um dos componentes de uma mistura heterogênea entre sólido e líquido. Sendo assim, o método adequado para separar a mistura entre Mg (OH2(s) e íons Ca2+ (aq) é a filtração.
Alternativa: A
QUESTÃO 93
Moradores do Brooklin, bairro de São Paulo, perdem o sono com um som alto, constante e estridente. O barulho é causado por anfíbios anuros trazidos do Caribe, da espécie Eleutherodactylus jahnstonei, que têm tamanho um pouco maior que o de um grão de feijão e que encontraram na capital um ambiente favorável. Cientistas foram até o local e encontraram esses animais nos jardins das casas.
Pererecas-assobiadoras tiram o sono de moradores do Brooklin. Disponível em: http://g1.gIobo.com. Acesso em: 26 mar. 2015 (adaptado).
Ao emitirem o som estridente, esses anfíbios
(A) indicam que estão fora de seu hábitat natural.
(B) alertam para a presença de poluição urbana.
(C) sinalizam a existência de superpopulação.
(D) direcionam insetos para sua alimentação.
(E) atraem fêmeas para o acasalamento.
Resolução:
A vocalização realizada pelos anfíbios é um comportamento ligado à seleção sexual e que aumenta a proximidade dos casais, permitindo sucesso reprodutivo.
Alternativa: E
QUESTÃO 94
A hidroxiapatita, Ca5(PO4)3OH, é um mineral constituinte do esmalte dos dentes. Entre as diversas reações que ocorrem no meio bucal, encontram-se em equilíbrio as reações de desmineralização e mineralização da hidroxiapatita em meio aquoso, ilustradas a seguir. A desmineralização está associada à fragilização do esmalte do dente e à formação de cáries.
O uso de creme dental pode minimizar a perda da hidroxiapatita. O quadro apresenta o agente de polimento e o pH de alguns cremes dentais comerciais.
Considerando o equilíbrio químico envolvido, qual creme dental promove a maior desmineralização do esmalte do dente?
(A) I
(B) II
(C) III
(D) IV
(E) V
Resolução:
O aumento da concentração do reagente desloca o equilíbrio químico no sentido de consumo da hidroxiapatita (sentido direto ou desmineralização).Valores de pH mais baixos apresentam maiores concentrações de straight H to the power of plus. Desse modo, o creme dental IV é o que promove a maior desmineralização.
Alternativa: D
QUESTÃO 95
A tirinha ilustra esquimós dentro de um iglu, habitação de formato hemisférico construída durante o inverno a partir de neve ou blocos de gelo. Essa estrutura de construção se justifica pelo fato de esse povo habitar as regiões mais setentrionais da Groenlândia, Canadá e Alasca.
LAERTE. Disponível em: https://artedafisicapibid.blogspot.com. Acesso em: 4 dez. 2021 (adaptado).
Na tirinha, a geladeira é necessária para fazer gelo porque
(A) a temperatura interna do iglu é maior que a de solidificação da água.
(B) a umidade dentro do iglu dificulta o processo de mudança de fase da água.
(C) o ar dentro do iglu é isolante térmico, dificultando a perda de calor pela água.
(D) a temperatura uniforme no interior do iglu impede as correntes de convecção.
(E) a pressão do ar no interior do iglu é baixa, dificultando a solidificação da água.
Resolução:
O gelo atua como um isolante térmico, o que permite que a temperatura interna de um iglu, mesmo com temperaturas externas abaixo de 0 °C, permaneça mais amena, geralmente acima de 0 °C. Assim, seria necessário o uso de uma geladeira para solidificar a água dentro do iglu.
Alternativa: A
QUESTÃO 96
Os pesticidas naturais vêm sendo utilizados no controle de pragas e doenças agrícolas como substituintes de pesticidas sintéticos tradicionais, por serem menos nocivos ao ambiente, biodegradáveis e minimizarem custos e riscos relativos à lavoura. Por exemplo, os compostos 1 e 2 estão envolvidos nas respostas de defesa das plantas. Os grupos funcionais presentes nesses compostos são importantes para as suas propriedades no controle de pragas.
PINTO-ZEVALLOS, D. M.; ZARBIN, P. H. G. A química na agricultura: perspectivas para o desenvolvimento de tecnologias sustentáveis. Química Nova, n. 10, 2013 (adaptado).
Qual é a função orgânica correspondente ao grupo funcional comum presente nesses dois compostos?
(A) Ácido carboxílico.
(B) Cetona.
(C) Alceno.
(D) Álcool.
(E) Fenol.
Resolução:
A função orgânica correspondente ao grupo funcional comum presente nesses dois compostos é o ácido carbxílico.
Alternativa: A
QUESTÃO 97
Utilizando-se um mesmo meio nutritivo, três gêneros bacterianos diferentes foram submetidos ao cultivo em tubos de ensaio. Após certo período de crescimento da cultura bacteriana em condições físico-químicas ideais, observou-se que o padrão de distribuição das células (representadas por pontos na figura) ao longo dos tubos era diferente em cada um dos casos.
Em relação ao metabolismo energético, os microrganismos presentes nos tubos 1, 2 e 3 são classificados, respectivamente, como
(A) anaeróbio facultativo, anaeróbio estrito e aeróbio estrito.
(B) anaeróbio facultativo, aeróbio estrito e anaeróbio estrito.
(C) aeróbio estrito, anaeróbio estrito e anaeróbio facultativo.
(D) anaeróbio estrito, aeróbio estrito e anaeróbio facultativo.
(E) aeróbio estrito, anaeróbio facultativo e anaeróbio estrito.
Resolução:
No tubo 1, observa-se a proliferação de bactérias aeróbias na parte superior, na qual há maior exposição ao oxigênio. No tubo 2, a proliferação ocorre no fundo, indicando a presença de bactérias anaeróbias, adaptadas a ambientes sem oxigênio. Já no tubo 3, há proliferação bacteriana ao longo de toda a extensão, com uma concentração um pouco maior na parte superior. Esse padrão sugere a presença de bactérias facultativas, que conseguem sobreviver em ambientes com baixa concentração de oxigênio, mas preferem áreas em que o oxigênio é mais abundante, aproveitando-o para se proliferar mais intensamente.
Alternativa: C
QUESTÃO 98
As placas que indicam saída de emergência brilham no escuro, pois apresentam substâncias que fosforecem na cor amarelo-esverdeada após exposição à luz ambiente, conforme a figura.
Esse fenômeno ocorre pela presença do sulfeto de zinco (ZnS), dopado com prata ou cobre, na superfície da placa.
Zinc Sulphide Phosphorescense. Disponível em: https://physicsopenlab.org. Acesso em: 8 nov. 2023 (adaptado).
O aparecimento do brilho nessas condições ocorre como consequência de
(A) colisões interatômicas.
(B) coloração dos átomos.
(C) transições eletrônicas.
(D) reações nucleares.
(E) reflexão da luz.
Resolução:
De acordo com o modelo de Bohr, o aparecimento do brilho nessas condições ocorre como consequência das transições eletrônicas realizadas pelos elétrons.
Segundo Bohr, ao saltar de uma órbita estacionária para outra, o elétron emite ou absorve uma quantidade bem-definida de energia.
Esses saltos entre órbitas foram denominados transições eletrônicas ou saltos quânticos.
Alternativa: C
QUESTÃO 99
Indústrias farmacêuticas e instituições científicas têm trabalhado no desenvolvimento de diferentes vacinas contra a covid-19. Em algumas dessas vacinas, a principal estrutura antigênica é uma proteína de superfície viral chamada espícula (spike, em inglês). Essa proteína só existe em coronavírus, incluindo o SARS-CoV-2. Ela se liga a receptores de membrana específicos das células humanas por um mecanismo do tipo "chave-ferradura". Dessa forma, os vírus entram nas células, podendo se multiplicar e acarretar a doença.
O que são vacinas? Disponível em: www.cienciaviva.pt. Acesso em: 30 nov. 2021 (adaptado).
Nessas vacinas, essa proteína viral induz a
(A) produção de anticorpos específicos contra os vírus.
(B) imunidade passiva contra o desenvolvimento da doença.
(C) alteração genômica para formação da memória imunológica.
(D) neutralização direta dos vírus presentes na circulação sanguínea.
(E) modificação dos receptores de membrana específicos para o vírus.
Resolução:
As proteínas spike atuam como antígeno e induzem a produção de anticorpos específicos por meio do modelo “chave-fechadura”, no qual um anticorpo só se encaixa em um antígeno específico por suas formas tridimensionais se complementarem.
Alternativa: A
QUESTÃO 100
Em um experimento de laboratório, duas barras metálicas, A e B, são carregadas com cargas opostas e imersas em óleo. Farelo de milho é jogado sobre o óleo e, após um certo tempo, o farelo assume o formato das linhas de campo elétrico entre as barras. A figura representa a vista superior desse experimento.
ALMEIDA, M. A. T. Introdução às ciências físicas 2 — volume 4: módulo 4. Rio de Janeiro: Fundação CECIERJ, 2007 (adaptado).
Ao repetir o experimento colocando um cilindro metálico oco entre as placas, o esquema que representa o formato das linhas de campo assumido pelo farelo é:
(A)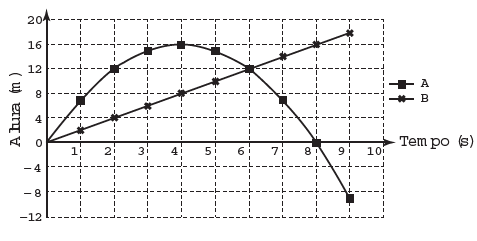 
(B) 
(C) 
(D) 
(E) 
Resolução:
As linhas de força do campo elétrico apontam para "fora" da carga positiva e para "dentro" da carga negativa. Como o campo elétrico no interior de um condutor em equilíbrio eletrostático é nulo, tem-se que a resposta correta é a da figura abaixo:
Alternativa: E
QUESTÃO 101
Placas solares comuns dependem de dias ensolarados para gerar energia. Mas podemos gerar eletricidade com a ajuda de gotas de chuva, revestindo placas solares com uma fina camada de grafeno. Os íons dissociados a partir da água da chuva open parentheses straight A to the power of straight m plus end exponent space straight e space straight B to the power of straight n minus end exponent close parentheses tornam a combinação grafeno e água da chuva um par perfeito para geração de energia. O processo requer apenas uma camada de grafeno para que grande quantidade de elétrons open parentheses straight e to the power of minus close parentheses se movimente ao longo da superfície.
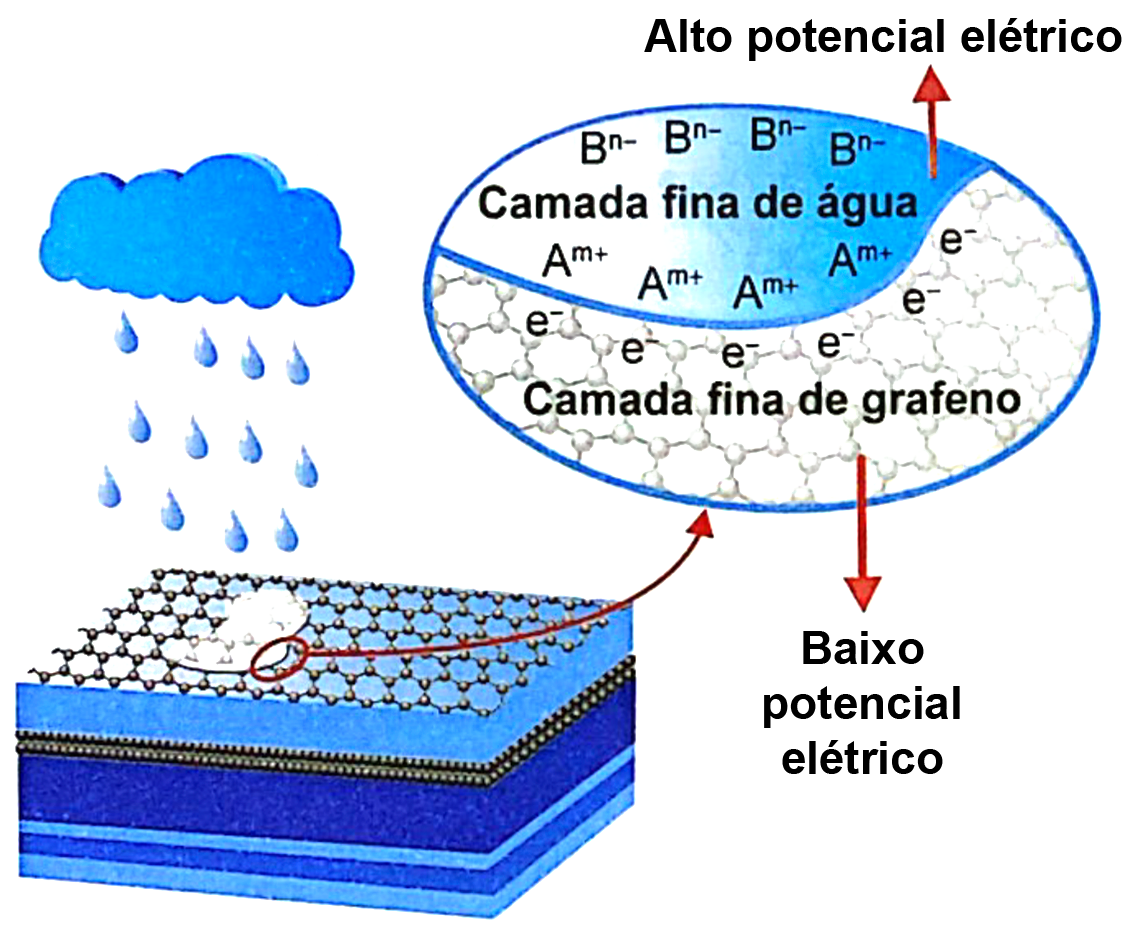
TANG, Q. et al. A Solar Cell that is Triggered by Sun and Rain. Angewandte Chemie International Edition, n. 55, 2016 (adaptado).
Ao produzir eletricidade em dias chuvosos, o grafeno
(A) oxida os cátions dissolvidos na água da chuva.
(B) impede a difusão da água através das placas solares.
(C) diminui a energia de ativação da reação no pseudocapacitor.
(D) forma um compósito não metálico com os íons na água da chuva.
(E) gera uma diferença de potencial pela interação dos elétrons com os cátions.
Resolução:
De acordo com a imagem da questão, a interação entre as camadas finas de grafeno (que possuem baixo potencial elétrico e funcionam como fonte de elétrons) e a camada de água (com alto potencial elétrico, fornecendo cátions e ânions) gera uma diferença de potencial elétrico, o que está relacionado à produção de eletricidade.
Alternativa: E
QUESTÃO 102
Um estudante comprou uma cafeteira elétrica de 700 W de potência e com capacidade de 0,5 L de água (500 g). Enquanto o café estava em preparação na capacidade máxima da cafeteira, ele marcou que demorou 3 minutos para a cafeteira ferver toda a água (100 °C) a partir da temperatura ambiente de 20 °C. Em seguida, para avaliar a eficiência da cafeteira, ele calculou esse tempo desprezando quaisquer perdas energéticas. É necessária 1 cal (4,2 J) para elevar em 1 °C a temperatura de 1 grama de água.
Qual a eficiência energética calculada pelo estudante?
(A) 100%
(B) 75%
(C) 60%
(D) 7,5%
(E) 5,1%
Resolução:
I) Determina-se a energia necessária para aquecer 500 g de água de 20 °C até 100 °C.
Q = m . c . Δt
500 . 1 . 80 = 40 000 Cal ou 168 000J
II) Para determinar a potência útil, tem-se:
Dado: 3 min = 180s
III) A eficiência é:
Sem alternativa correspondente, portanto.
QUESTÃO 103
O diagrama P-V a seguir representa o ciclo de Otto para um motor de combustão interna, como os motores a gasolina ou a etanol, utilizados nos automóveis.
As etapas representadas no diagrama estão descritas no quadro.
A transformação da energia térmica em energia útil ocorre na etapa
(A) II
(B) III
(C) IV
(D) V
(E) VI
Resolução
A energia térmica é transformada em energia útil quando uma máquina térmica realiza trabalho, ou seja, W > 0
O gás não realiza nem sofre trabalho em processos isocóricos. Analisando os processos adiabáticos (W – 0), tem´se:
ΔU = Q – W
ΔU = – W
Para que W – 0 , é necessário que ΔU = < 0 . Como a variação da energia interna depende diretamente da variação da temperatura, é necessário que ΔT < 0, ou seja, que a temperatura diminua. Isso ocorre da etapa 3 a 4.
Alternativa: C
QUESTÃO 104
Para os circuitos de maratonas aquáticas realizadas em mares calmos e próximos à praia, é montado um sistema de boias que determinam o trajeto a ser seguido pelos nadadores. Uma das dificuldades desse tipo de circuito é compensar os efeitos da corrente marinha. O diagrama contém o circuito em que deve ser realizada uma volta no sentido anti-horário. As quatro boias estão numeradas de 1 a 4. Existe uma corrente marinha de velocidade Vc, cujo módulo é 30 metros por minuto, paralela à praia em toda a área do circuito. Nas arestas mais longas, o nadador precisará nadar na direção apontada pelos vetores Vn dos pontos 1 até 2 e de 3 até 4. Considere que a velocidade do nadador é de 50 metros por minuto, em relação à água, durante todo o circuito.
Nessa situação, em quantos minutos o nadador completará a prova?
(A) 42
(B) 65
(C) 72
(D) 105
(E0 120
Resolução:
Trecho 1 - 2:
Vn2 = Vres2 + Vc2
502 = Vres2 + 302
Vres2 =1600
Vres = √1600
Vres = 40 m / min
Vm = ΔS
Δt
40 = 800
Δ12
Δ12 = 20 min
Trecho 2 - 3:
Vres = Vn - Vc
Vres = 50 - 30
Vres = 20 m /min
Vm = ΔS
Δt
40 = 800
Δ23
Δ23 = 20 min
Trecho 3 - 4:
Vn2 = Vres2 + Vc2
502 = 30s2 + Vres2
Vres2 =1600
Vres = √1600
Vres = 40 m / min
Vm = ΔS
Δt
40 = 800
Δ34
Δ34 = 20 min
Trecho 4 - 1:
Vn = Vres + Vc
Vres2 = 30 + 50
Vres =80 m/min
Vm = ΔS
Δt
80 = 400
Δ41
Δ41 = 5 min
Tempo total:
ΔtT = Δt12 + Δt23 + Δ734 + Δt41
ΔtT = 20 + 20 + 20 + 5
ΔtT = 65 min
Alternativa: B
QUESTÃO 105
O vírus linfotrópico de células T humanas tipo 1 (HTLV-1) é um retrovírus do mesmo grupo do vírus da imunodeficiência humana (HIV). Ambos são transmitidos da mesma forma e infectam as mesmas células de defesa do organismo, os linfócitos T. A diferença entre eles é que o HTLV-1 estimula o aumento da produção desses linfócitos, enquanto o HIV causa destruição dessas células.
ROMANELLI, L. C. F.; CARAMELLI, P.; PROIETTI, A. B. F. C. O vírus linfotrópico de células T humanas tipo 1 (HTLV-1): quando suspeitar da infecção? Revista da Associação Médica Brasileira, v. 56, 2010 (adaptado).
Uma possível consequência da infecção por HTLV-1 é o desenvolvimento de
Uma possível consequência da infecção por HTLV-1 é o desenvolvimento de
(A) aids.
(B) câncer.
(C) diabetes.
(D) hepatite B.
(E) hemorragia.
Resolução:
O vírus HTLV-1 é um retrovírus que estimula a proliferação de linfócitos humanos. Nesse sentido, esse vírus pode desencadear o desenvolvimento de câncer, uma doença decorrente da proliferação descontrolada de células no corpo humano.
Alternativa: B
QUESTÃO 106
Na tirinha, Calvin se divertia em um balanço antes de soltar-se dele e cair ao chão. Em sua fala, ele demonstra ter imaginado que permaneceria em movimento circular. Porém, a força gravitacional, que permanece atuando no garoto, modifica a direção de sua velocidade, fazendo com que ele chegue ao chão da maneira ilustrada no último quadrinho.
Qual vetor representa a força resultante exercida pelo chão sobre Calvin no exato momento em que ele toca o chão?
(A)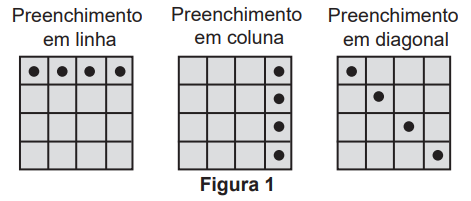 
(B) 
(C) 
(D) 
(E) 
Resolução:
A força resultante aplicada pelo chão sobre o garoto será a resultante entre a componente de atrito para a direita, contrária ao deslizamento ou tendência ao deslizamento, e a componente normal, perpendicular ao plano e para cima.
Sendo assim, a resultante será a diagonal representada pela alternativa A.
Alternativa: A
QUESTÃO 107
A fitorremediação é uma técnica que utiliza plantas para a remediação de ambientes contaminados. A descontamicação de solos pode ocorrer por descarte, absorção e metabolização, imobilização, extração ou volatilização do poluente, conforme representado na figura.
LUIZ, E. P. Avaliação dos métodos de fitorremediação [...] na remoção de chumbo, cobre e zinco. São Paulo: UFABC, 2016 (adaptado).
O método que retira o mercúrio de uma área contaminada, impedindo sua entrada na cadeia alimentar, é a
(A) fitoestabilização, ficando o mercúrio disponível sob a superfície das raízes das plantas.
(B) fitovolatilização, permitindo a retirada do mercúrio por plantas e a sua transferência para uma forma volátil.
(C) fitodegradação, com a degradação do mercúrio promovida por enzimas, contidas nas raízes, formando espécies menos tóxicas.
(D) fitoestimulação, com a remoção do mercúrio pela ação de microrganismos presentes nas raízes que absorvem e imobilizam o metal.
(E) fitoextração, em que plantas que acumulam o mercúrio são cultivadas nesses locais, e a biomassa rica no metal é retirada após o crescimento.
Resolução:
Na fitoextração, as plantas acumulam o mercúrio em sua biomassa, que, posteriormente, pode ser retirada do ambiente. Para evitar a biomagnificação e a entrada do mercúrio nos consumidores da cadeia alimentar, essa biomassa contaminada precisa ser removida e descartada de forma segura, como, por exemplo, por meio da incineração. Essas medidas impedem que o mercúrio retorne ao ambiente ou que seja consumido por animais que se alimentariam dessa planta. Com esse manejo, podemos evitar que o mercúrio entre na cadeia alimentar local.
Por outro lado, a alternativa "B", fitovolatilização, pode ser justificada pelo fato de que o processo envolve a conversão do mercúrio em uma forma volátil, que é liberada para a atmosfera, em vez de ser absorvida diretamente pela cadeia alimentar. Esse processo impede que o mercúrio se acumule na biomassa da planta ou no solo, evitando que seja ingerido por herbívoros ou outros organismos da cadeia alimentar. A volatilização transforma o contaminante em uma forma que não é facilmente assimilada por organismos terrestres, reduzindo a possibilidade de biomagnificação (acúmulo do poluente ao longo da cadeia alimentar). Em áreas contaminadas, como a mencionada no texto, a fitorremediação via fitovolatilização de metais pesados, como o mercúrio, é uma técnica que pode ser vantajosa para evitar contaminações em ecossistemas locais, sem risco imediato de biomagnificação, já que o mercúrio volátil se dispersa para a atmosfera e não fica disponível para consumo por organismos da cadeia alimentar. No entanto, esse método, embora eficiente para remover o mercúrio do solo, pode transferi-lo para a atmosfera, tornando-se uma nova fonte de poluição.
A técnica da alternativa "E" é mais utilizada na fitorremediação, pois permite a remoção eficaz do mercúrio do solo e impede sua entrada na cadeia alimentar, desde que a biomassa contaminada seja descartada de forma segura. Embora a alternativa "B" (fitovolatilização) também evite a biomagnificação, ela libera mercúrio para a atmosfera, criando uma nova fonte de poluição.
Alternativa: E
QUESTÃO 108
Brasil fecha 2020 entre os maiores recicladores de latas de alumínio
A bauxita contém alumina open parentheses Al subscript 2 straight O subscript 3 close parentheses, que é a matéria-prima para produção do alumínio (Al). De forma geral, são necessários 50 kg de bauxita para produzir 10 kg de alumínio. O Brasil fechou 2020 como um dos principais líderes mundiais em reciclagem de latas de alumínio. De acordo com levantamento da Associação Brasileira dos Fabricantes de Latas de Alumínio (Abralatas), o país obteve um índice de reciclagem de 97,4%, de um total de 4 comma 0 space cross times space 10 to the power of 5 toneladas de latas vendidas. Considere que a lata é constituída de alumínio puro.
Disponível em: https://agenciabrasil.ebc.com.br. Acesso em: 30 nov. 2021 (adaptado).
Levando em conta apenas a reciclagem de latas, qual é o valor mais próximo da massa de bauxita, em tonelada, que deixou de ser extraída da natureza em 2020 no Brasil?
(A) 1,0 x 104 ton
(B) 3,9 x 105 ton
(C) 5,0 x 104 ton
(D) 1,9 x 106 ton
(E) 2,0 x 107 ton
Resolução:
Em 2020, o Brasil reciclou 97,4% de um total de 5,0 x 105 (de latas) de alumínio. Assim, a massa de alumínio reciclado nesse ano foi igual a:
m = (0,974) . (4,0 . 105 = 3,896 . 105 t
Para produzir 10 kg de alumínio, são necessários 50 kg de bauxita.
Aplicando regra de três temo:
10 kg alumínio ------- 50 kg bauxita
3,896 . 105 ------- m
m = 19,84 . 105t = 1,9 . 106 t bauxita
Assim, a massa de bauxita que deixou de ser extraída da natureza em 2020 é
Alternativa: D
QUESTÃO 109
O LED é um dispositivo eletrônico que conduz corrente elétrica em um único sentido, sendo caracterizado por uma tensão e uma corrente máxima de funcionamento, Imáx. Um LED acende apenas se a corrente que o percorre está no sentido permitido e se a diferença de potencial à qual está submetido é igual ou superior à sua tensão de funcionamento. A figura ilustra o símbolo do LED usado na representação de circuitos.
Um estudante de física analisa as propriedades do LED em um circuito simples de corrente contínua. Ele dispõe dos seguintes materiais: uma bateria ideal de 4,5 V; dois LEDs de tensão 3,0 V e Imax = 1,0 mA cada; e dois resistores de 1,5 kΩ por cada.
O circuito que o estudante pode montar, para que ambos os LEDs fiquem acesos e cada um seja percorrido por Imáx, é
(A) 
(B) 
(C) 
(D) 
(E) 
Resolução:
Como cada LED precisa ser percorrido por uma corrente de 1 mA, os LEDs devem estar ligados em paralelo e, assim, a corrente total será de 2 mA.
Logo, o resistor que acompanha o LED deve estar em série com cada um para que sua d.d.p seja de 1,5 V.
Esses dois conjuntos são colocados em paralelo com a fonte ideal.
Alternativa: B
QUESTÃO 110
Uma caixa decorativa utiliza duas pequenas lâmpadas, L1 (6 v – 9W), ligadas em série a uma bateria de tensão V.QR.Um fio resistivo QR, de 48 centímetros, está ligado em paralelo à bateria. Cinco pontos, A, B, C, D e E, dividem o fio QR em seis segmentos de comprimentos iguais. O circuito também tem um amperímetro com dois terminais. Um dos terminais (P) está ligado ao fio entre as duas lâmpadas. O outro terminal (S) está livre e será ligado ao fio QR. Dependendo do ponto em que esse terminal livre for conectado, ocorrerá a mudança na tensão à qual as lâmpadas são submetidas. Os demais fios do circuito têm resistências elétricas desprezíveis. A figura ilustra esse circuito.
Em qual desses pontos o amperímetro deve ser conectado para que as lâmpadas acendam exatamente segundo as especificações de tensão e potência elétricas fornecidas?
(A) A
(B) B
(C) C
(D) D
(E) E
Resolução:
As lâmpadas L1 e L2 estarão sujeitas a diferenças de potenciais proporcionais aos resistores que estarão em paralelo a essas lâmpadas, sendo assim, como a d.d.p. para funcionamento da lâmpada L1 é de 6 V e da lâmpada L2 de 12 V, tem-se que as resistências em paralelo devem manter a proporção de 1 para 2.
Portanto, o terminal S deve ser ligado em B para se ter duas partes paralelas a L1 e quatro partes paralelas a L2.
Com o terminal na posição B, tem-se uma ponte de fio equilibrada, o que faz com que as lâmpadas estejam em paralelo com as respectivas partes do fio QR.
Alternativa: B
QUESTÃO 111
O biogás é uma altemativa energética muito importante, pois, além de reduzir a dependência por combustíveis fósseis, sua obtenção pode ser realizada a partir de resíduos da produção agroindustrial. Considere que o biogás produzido em um empreendimento de suinocultura contém 70% em volume de metano (massa molar 16 g/mol; volume molar 22 L/mol). Ele será utlizado para geração de energia em substituição ao etanol (massa molar 46 g/mol) em um gerador no qual 1 m³ de biogás de origem suína substitui 0,59 L de etanol anidro (densidade 0,78 g/mL).
Nessas condições, a massa de metano necessária para substituir 10 mol de etanol na produção de energia é mais próxima de
(A) 300 g.
(B) 400 g.
(C) 510 g.
(D) 590 g.
(E) 720 g.
Resolução:
Cálculo da massa de etanol substituída a partir da massa molar:
1 mol de etanol ---- 46 g de etanol
10 mol de etanol ---- m etanol
m etanol = 460 g de etanol
Cálculo do volume de etanol a partir da densidade:
0,78 g de etanol --- 1 mL de etanol
460 g de etanol ---- V etanol
V etanol = 590 mL de etanol = 0,590 L de etanol
Segundo o texto, 1 m³ de biogás substitui 0,59 L de etanol.
Sendo o biogás constituído de 70% de metano, há 0,70 m³ ou 700 L de CH subscript 4.
Cálculo do número de mols de metano:
22L de CH4 ---- 1 mol de CH4
700 L de CH4 ---- n CH4
nCH4 = 31,8 mol de CH4
Cálculo da massa de metano a partir da massa molar:
1 mol de CH4 ---- 16 g de CH4
31,8 mol de CH4 ---- mCH4
mCH4 = 508,8 g de CH4 = 510 g
Alternativa: C
QUESTÃO 112
A nimesulida é um fármaco pouco solúvel em água, utilizado como anti-inflamatório, analgésico e antitérmico. Essa substância pode ser convertida em uma espécie eletricamente carregada, de maior solubilidade em água, mediante o tratamento com uma base de Brönsted-Lowry, isto é, uma espécie química capaz de capturar um próton open parentheses straight H to the power of plus close parentheses. Na figura são apresentados os grupamentos presentes na estrutura química da nimesulida.
GONÇALVES, A. A. et al. Contextualizando reações ácido-base de acordo com a teoria protônica de Brönsted-Lowry usando comprimidos de propanolol e nimesulida. Química Nova, n. 3, 2013 (adaptado).
Na estrutura desse fármaco, o grupamento capaz de reagir com a base de Brönsted-Lowry é o grupo
(A) sulfonamida.
(B) metila.
(C) fenila.
(D) nitro.
(E) éter.
Resolução:
O conceito de ácido-base segundo Brönsted-Lowry diz que ácidos são substâncias capazes de doar straight H+, bases, substâncias capazes de receber straight H+. Na estrutura da nimesulida, o grupamento capaz de reagir com uma base de Brönsted-Lowry, ou seja, capaz de atuar como um ácido de Brönsted-Lowry e doar straight H+ é a sulfonamida, que perderia o hidrogênio ligado ao nitrogênio.
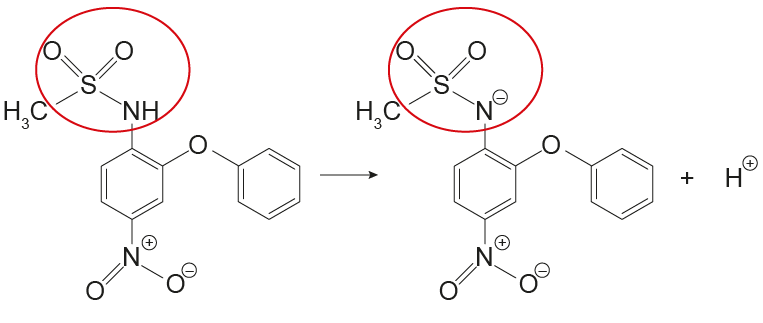
Alternativa: A
QUESTÃO 113
O desenvolvimento da biotecnologia e da clonagem gênica em procariotos fez com que a produção de proteínas se tornasse mais intensa, rápida e econômica. Para a produção de hormônios, enzimas e proteínas de resistência a drogas, uma variação da técnica de reação em cadeia pela polimerase (PCR, na sigla em inglês) utiliza a enzima transcriptase reversa (RT-PCR), que sintetiza moléculas de DNA complementares a partir de fitas de RNA.
Nesse contexto, essa técnica é importante para detectar genes
(A) expressos.
(B) plasmidiais.
(C) bacterianos.
(D) dominantes.
(E) autossômicos.
Resolução:
A técnica de RT-PCR utiliza o RNA derivado de genes ativos, permitindo a detecção específica de genes que estão sendo expressos no momento da análise.
Alternativa: A
QUESTÃO 114
Nos automóveis, é importante garantir que o centro de massa (CM) de cada conjunto roda/pneu coincida com o seu centro geométrico. Esse processo é realizado em uma máquina de balanceamento, na qual o conjunto roda e pneu é colocado para girar a uma velocidade de valor constante. Com base nas oscilações medidas, a máquina indica a posição do centro de massa do conjunto, e pequenas peças de chumbo são fixadas em lugares específicos da roda até que as vibrações diminuam. Durante o treinamento de sua equipe, a fim de corrigir a posição do centro de massa indicada pela máquina, um mecânico apresenta o esquema a seguir, com cinco possíveis pontos da roda para posicionar uma peça de chumbo.
Em qual ponto deve ser fixada a peça de chumbo para corrigir a posição do centro de massa desse conjunto roda/pneu?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Resolução:
Nessa situação, para diminuir as vibrações, é necessário deslocar o centro de massa no centro do conjunto roda/pneu.
Para alterar a posição do centro de massa de um corpo, pode-se adicionar um peso na direção para a qual se deseja deslocar o centro de massa. Portanto, o ponto 3 é o mais recomendado para fixar a peça de chumbo e deslocar o centro de massa para o meio do conjunto roda/pneu.
Alternativa: C
QUESTÃO 115
O soro caseiro serve para combater a desidratação por meio da reposição da água e sais minerais perdidos, por exemplo, por diarreia. Uma receita simples para a sua preparação consiste em utilizar duas colheres grandes (de sopa) de açúcar e duas colheres pequenas (de café) de sal de cozinha, dissolvidos em 2 L de água fervida, obtendo-se uma solução com concentração de íon sódio de 1,4 mg/mL.
Considere as massas molares: NaCl = 58,5 g/mol; Na = 23 g/mol.
Qual é o valor mais próximo da massa, em grama, de cloreto de sódio presente em uma única colher pequena?
(A) 0,7 g
(B) 1,8 g
(C) 2,8 g
(D) 3,6 g
(E) 7,0 g
Resolução:
CNa+ = 1,4 mg . mL-1 = 1,4 g . L-1
Pelo enunciado, o soro foi preparado colocando-se 2 colheres de sal de cozinha em 2 L de água, o que equivale a 1 colher por litro
(1,4 g Na+ . L-1)
1 mol NaCl ---- 1mol Na+
558,5 g ---- 23 g
x = 3,56 g = 3,6
Alternativa: D
QUESTÃO 116
Apesar de os animais representados no cladograma compartilharem um mesmo ancestral, eles se caracterizam por distintos padrões de reprodução ou de nutrição dos embriões e descendentes.
DIXSON, A. F. Mammalian Sexuality: The Act of Mating and the Evolution of Reproduction. Disponível em: www.cambridge.org. Acesso em: 2 jul. 2024 (adaptado).
Ao longo do processo evolutivo, percebem-se, entre esses animais, perdas e ganhos nos padrões citados que envolvem o(a)
(A) aumento no número de descendentes por ninhada.
(B) mudança no tipo de fecundação de externa para interna.
(C) redução da versatilidade de reprodução, que se torna unicamente sexuada.
(D) desenvolvimento embrionário, que passa do meio aquático para o terrestre.
(E) diminuição da vesícula vitelínica, associada ao desenvolvimento da lactação.
Resolução:
Assim como aves e répteis, durante o desenvolvimento embrionário, todos os grupos de mamíferos formam a vesícula vitelínica, um anexo capaz de armazenar e disponibilizar nutrientes ao embrião. Todavia, os mamíferos contam com glândulas mamárias, fundamentais para o abastecimento dos filhotes após o nascimento. Desse modo, para garantir a nutrição dos indivíduos, há uma tendência de diminuição da vesícula vitelínica, em resposta a um incremento da função associada à lactação.
Alternativa: E
QUESTÃO 117
Uma ambulância em alta velocidade com a sirene ligada desloca-se em direção a um radar operado por uma pessoa. O radar emite ondas de rádio com frequência f0, que são refletidas pela dianteira da ambulância, retornando para o detector com frequência fr. A percepção do operador do radar, em relação ao som emitido pela sirene, é de que este se altera à medida que a ambulância se aproxima ou se afasta. Durante a aproximação, como o operador percebe o som da sirene e qual é a relação entre as frequências fr e f0 medidas pelo radar?
(A) Mais grave do que o som emitido e fr < f0.
(B) Mais agudo do que o som emitido e fr < f0.
(C) Mais agudo do que o som emitido e fr = f0
(D) Mais agudo do que o som emitido e fr > f0
(E) Mais grave do que o som emitido e fr > f0
Resolução:
A situação envolve fonte e receptor de ondas com um movimento relativo entre si. Logo, trata-se de uma situação de efeito Doppler.
Considerando a ambulância como a fonte da onda sonora, aproximando-se do ouvinte (operador do radar) em repouso:
Sendo v a velocidade da onda sonora.
Sendo o fator de multiplicação maior que 1. Desse modo, o operador ouve o som mais agudo do que aquele emitido pela ambulância:
Em relação à onda de rádio emitida pelo radar, ela sofrerá duas mudanças de frequência: ao ser emitida pela fonte em repouso e depois ao ser refletida pela ambulância.
a) Onda de rádio emitida pelo operador em repouso e recebida pela ambulância que se aproxima em movimento:
Sendo o Verc a velocidade da ambulância, f0 a frequência da onda de rádio emitida pelo operador, de acordo com o enunciado.
Esta é a frequência aparente recebida pela ambulância. Esta frequência será refletida pelo veículo para o operador do radar. Então, tem-se a seguinte situação de efeito Doppler:
b) Onda refletida pela ambulância que se aproximada do receptor (operador) em repouso:
Sendo o Vfonte a velocidade da ambulância, fr a frequência da onda de rádio recebida pelo operador, de acordo com o enunciado.
Deste modo:
fr < f0
Cabe destacar que a onda de rádio é uma onda eletromagnética que viaja à velocidade da luz (c = 3,0 . 108 m/s). Sendo assim, na resolução deveria constar o efeito Doppler relativístico, com suas devidas correções. fr > 10
Alternativa: D
QUESTÃO 118
Mirascópio 3D: produtor de ilusão instantânea
O equipamento ilustrado na figura, de dimensões apresentadas no esquema, é composto por dois espelhos côncavos straight E subscript 1 e straight E subscript 2, apoiados um sobre o outro por suas bordas, de tal forma que o vértice de straight E subscript 1 coincide com o foco de straight E subscript 2 e vice-versa. Na abertura circular de straight E subscript 2, é formada uma imagem tridimensional de um objeto posicionado sobre o vértice de straight E subscript 1. Essa imagem é formada a partir dos raios procedentes do objeto, refletidos por straight E subscript 2 space straight e space straight E subscript 1, respectivamente, conforme o esquema. Os observadores julgam visualizar o objeto quando estão, de fato, visualizando sua imagem. O efeito só é possível porque as superfícies de ambos os espelhos são de extrema qualidade.
A natureza da imagem formada e a distância vertical entre cada ponto objeto e seu correspondente ponto imagem são
(A) real e 5 cm.
(B) real e 3,8 cm.
(C) real e 7,6 cm.
(D) virtual e 7,6 cm.
(E) virtual e 3,8 cm.
Resolução:
A imagem formada pelo mirascópio 3D está sendo projetada, ou seja, é uma imagem real. Analisando a figura proposta na questão, a distância vertical entre cada ponto objeto e seu correspondente ponto imagem é de:
D = 3,8 + 3,8
D = 7,6 cm
Alternativa: C
QUESTÃO 119
Muitas pessoas ainda se espantam com o fato de um passageiro sair ileso de um acidente de carro enquanto o veículo onde estava teve perda total. Essas pessoas talvez considerem, equivocadamente, que os carros mais seguros são os que têm as estruturas mais rígidas, ou seja, estruturas, que durante uma colisão, apresentam menor deformação. Na verdade, o que ocorre é o contrário. Por isso, a partir de 1958, passaram a ser produzidos carros com partes que se deformam facilmente.
DAY, C. Crumple Zones. Disponível em: https://pubs.aip.org. Acesso em: 2 jul. 2024 (adaptado).
Assim, além dos cintos de segurança e dos airbags, os carros modernos passaram a contar com o dispositivo de segurança conhecido como crumple zone (região deformável, em inglês), conforme a figura.
Momentum and Car safety. GCSE Physics Revision. Disponível em: www.shalom-education.com. Acesso em: 5 jul. 2024 (adaptado).
Considerando o carro, seus ocupantes e o muro da figura como um sistema isolado, o crumple zone aumenta a segurança dos passageiros porque, durante uma colisão, a deformação da estrutura do carro
(A) aciona os airbags do veículo.
(B) absorve a energia cinética do sistema.
(C) consome a quantidade de movimento do sistema.
(D) cria uma barreira de proteção para seus ocupantes.
(E) diminui a velocidade do centro de massa do sistema.
Resolução:
Neste acidente, houve uma colisão inelástica, na qual a energia cinética foi totalmente convertida em outras formas de energia. A deformação do veículo gasta parte dessa energia e, com isso, o crumple zone aumenta a segurança dos passageiros, reduzindo o impacto sofrido por eles.
Alternativa: B
QUESTÃO 120
Células a combustível microbianas (CCM) são capazes de gerar eletricidade a partir de águas residuárias urbanas e agroindustriais. As CCM são compostas de duas câmaras. Numa delas, onde ocorre o tratamento da matéria orgânica, as bactérias eletrogênicas crescem formando um biofilme e se alimentam dos poluentes presentes no efluente. Ao se alimentarem, essas bactérias geram uma corrente elétrica que percorre o material sobre o qual elas formaram o biofilme. Um fio condutor externo possibilita a migração dessa corrente para uma segunda câmara, promovendo uma reação química. A figura esquematiza uma CCM e as reações envolvidas.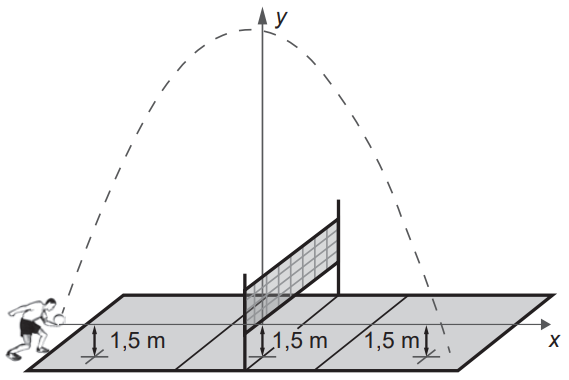
QUINTO, A. C. Biobactérias geram eletricidade a partir de esgoto sanitário e efluentes agroindustriais.
Disponível em: https://jornal.usp.br Acesso em: 1 dez. 2021 (adaptado).
Qual das equações representa a reação global que ocorre durante o funcionamento dessa CCM?
(A) CH3COO- (aq) + O2(g) → 2CO2(g) + 3H+ (aq)
(B) CO2(g) + O2(g) + H+ (aq) → H2O(l) + CH3COO- (aq)
(C) CH3COO- (aq) + H+ (aq) + 202(g) → 2CO2(g) + 2H2O(l)
(D) CH3COO- (aq) + 6H2O(l) → 2CO2(g) + 15H+ (aq)
(E) 2CO2(g) + 11H+ (aq) + O2(g) → CH3COO- (aq) + 4H2O(l)
Resolução:
Equações fornecidas:
CH3COO- (aq) + 2H2O(l) → 2CO2(g) + 7H+(aq) + 8 e -
4H+ (aq) + O2(g) + 4e- → 2H2O(l)
Deve-se multiplicar a segunda equação por 2 para obter a mesma quantidade de elétrons (cedidos e recebidos) e então somar as duas equações:
CH3COO- (aq) + 2H2O(l) → 2CO2(g) + 7H+ (aq) + 8 e -
8H+(aq) + 2H2O(g) → + 8 e – 4H2O(l)
CH3COO- (aq) + H+ (aq) + 2O(g) → 2CO2(g) + 2HO(l)
Alternativa: C
QUESTÃO 121
No senso comum, considera-se, ainda hoje, que compostos orgânicos são substâncias presentes nos seres vivos. Na Química, a expressão "compostos orgânicos" tem um uso histórico de mais de 200 anos, adquirindo diferentes conotações ao longo do desenvolvimento dessa ciência. Atualmente, atribui-se a essa expressão outro significado.
A concepção científica atual define esses compostos como substâncias
(A) benéficas à saúde humana.
(B) capazes de serem biodegradadas.
(C) formadas a partir de gás carbônico.
(D) produzidas sem o uso de agrotóxicos.
(E) contendo carbono como elemento principal.
Resolução:
Segundo a concepção científica atual, definida pelo químico alemão August Kekulé, Química Orgânica é o ramo da Química que estuda os compostos de carbono.
Alternativa: E
QUESTÃO 122
Metabolismo de procariontes
O esquema representa a ação de organismos no ciclo do nitrogênio e no ciclo do carbono. Os números correspondem a algumas etapas dos dois ciclos distintos.
Disponível em: https://pt.khanacademy.org. Acesso em: 27 jun. 2024 (adaptado).
Em qual etapa numerada ocorre uma transformação redox como a que ocorre nos procariontes nitrificantes?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Resolução:
Transformação redox nos procariontes nitrificantes:
NH3 → NO-2
NOXN = - 3 → NOXN = + 3
NH3 = -3 → NOX
NH3 → NO-2
NOXN = - 3 → N0XN = + 5
Observa-se que ocorre uma oxidação (aumento no número de oxidação) em relação ao nitrogênio.
O processo que se assemelha à transformação redox nos procariontes nitrificantes é a etapa numerada 5, em que os procariontes decompositores convertem o carbono fixado (estado oxidativo menor do que +4) em CO2, que apresenta o maior estado oxidativo do elemento carbono (+4). Desse modo, o carbono sofre uma oxidação.
Alternativa: E
QUESTÃO 123
Um dos agentes que mais contribui para a poluição do ar é o automóvel a combustão interna. Em áreas urbanas, isso é demonstrado dramaticamente pela fumaça fotoquímica, resultante da interação entre óxidos de nitrogênio, hidrocarbonetos e luz solar, para formar produtos de oxidação, que causam irritação aos olhos, ao aparelho respiratório e danos às plantas. As condições de operação de motores a combustão, como a razão da mistura ar/combustível no cilindro, influenciam na composição dos gases lançados pelo escapamento na atmosfera. O gráfico ilustra a variação nas composições dos principais gases, dióxido de carbono CO2, hidrocarbonetos (HC), monóxido de carbono (CO), monóxido de nitrogênio (NO) e oxigênio molecular (O2), emitidos por um motor a gasolina, em diferentes razões ar/combustível, em massa.
RANGEL, M. C.; CARVALHO, M. F. A. Impacto dos catalisadores automotivos no controle da qualidade do ar. Química Nova, v. 26, 2003 (adaptado).
Na condição de razão ar/combustível igual a 18, haverá uma emissão
(A) baixa de O2 e alta de NO.
(B) baixa de NO e alta de HC.
(C) baixa de CO e alta de CO2.
(D) baixa de HC e alta de CO.
(E) baixa de CO2 e alta de HC
Resolução:
De acordo com a análise do gráfico fornecido pela questão:
Com a razão ar/combustível igual a 18 (linha vermelha traçada no gráfico), a emissão de CO é baixa (próxima de zero), enquanto a emissão de CO2 é alta (acima de 12%).
Alternativa: C
QUESTÃO 124
A saúde do professor: acústica arquitetônica
Dentre os parâmetros acústicos que afetam a inteligibilidade dos sons emitidos em ambientes fechados, destacam-se o ruído de fundo do ambiente e o decréscimo do nível sonoro com a distância da fonte emissora. Assim, sentar-se no fundo da sala de aula pode prejudicar a aprendizagem dos estudantes, por impedir que eles distingam, com precisão, os sons emitidos, diminuindo a inteligibilidade da fala de seus professores. Considere a situação exemplificada pelo infográfico: à distância de 1 metro, o nível sonoro da fala de um professor é de 60 dB e diminui com a distância. Considere, ainda, que o ruído de fundo nessa sala de aula pode chegar a 45 dB e que, para ser compreendida, o nível sonoro da fala do professor deve estar 5 dB acima desse ruído.
Disponível em: www.ufrrj.br. Acesso em: 2 dez. 2021 (adaptado).
Para um valor máximo de ruído de fundo, a maior distância que um estudante pode estar do professor para que ainda consiga compreender sua fala é mais próxima de
(A) 3,0 m.
(B) 4,5 m.
(C) 6,5 m.
(D) 8,0 m.
(E) 9,5 m.
Resolução:
Considerando que a fala do professor deve estar 5 dB acima do ruído de fundo da sala, é preciso que a fala emitida de 60 dB chegue aos alunos a um nível de 50 dB. Analisando o gráfico do nível sonoro e da distância, tem-se:
3m.
Para que ainda consiga compreender a fala do professor, a distância máxima que o aluno deve manter dele é de
Alternativa: A
QUESTÃO 125
Uma agricultora, com a intenção de comercializar o milho recém-colhido, testou uma forma de preservar o sabor adocicado do seu produto. O melhor resultado foi obtido quando ela imergiu as espigas em água fervente durante alguns minutos e, em seguida, em água gelada. Com esse procedimento, parte da glicose do milho não foi transformada em amido, mantendo o seu sabor adocicado.
Utilizando esse procedimento, o sabor foi conservado porque houve
(A) desnaturação enzimática pela alta temperatura.
(B) conversão de nutrientes pela redução de temperatura.
(C) degradação das reservas nutritivas pelo choque térmico.
(D) impedimento da entrada de oxigênio pela fervura da água.
(E) desidratação dos grãos por causa da alteração da temperatura.
Resolução:
Enzimas são proteínas catalíticas que, quando submetidas a temperaturas acima da ideal, sofrem o processo de desnaturação, o qual consiste na alteração da estrutura da molécula, comprometendo sua função.
Diante disso, entende-se que, no procedimento executado pela agricultora, ao imergir a espiga em água fervente, ocorreu a desnaturação da enzima responsável pela conversão da glicose em amido, auxiliando a preservação do sabor adocicado do milho.
Alternativa: A
QUESTÃO 126
Aquecedores solares são equipamentos utilizados para o aquecimento de água pelo calor do Sol. São compostos por coletores solares, nos quais ocorre o aquecimento da água, e por um reservatório térmico, em que é armazenada a água quente para ser utilizada posteriormente. A figura ilustra esquematicamente como funciona esse equipamento.
5 dicas de instalação de aquecedor solar.
Disponível em: https://instaline.com.br. Acesso em: 3 nov. 2023 (adaptado).
O processo pelo qual ocorre transferência de calor dos coletores solares para o reservatório térmico é a
(A) difusão.
(B) absorção.
(C) condução.
(D) irradiação.
(E) convecção.
Resolução:
Os coletores solares captam a radiação solar e transformam essa energia em calor. Essa captação é feita através da irradiação. A superfície do coletor é feita de materiais que absorvem bem o calor, como o cobre ou o alumínio, muitas vezes pintados com cores escuras para aumentar a absorção de energia solar.
Dentro dos coletores solares, circula um fluido que absorve o calor captado. Nos coletores, a transferência de calor para o fluido ocorre por condução: o calor é transferido do material absorvente para o fluido em contato com ele.
Então, a água aquecida é transportada dos coletores para o reservatório térmico, onde cede calor para a água que será utilizada. Quando o sistema é montado de forma que o coletor solar fique abaixo do reservatório térmico, como se pode perceber na imagem do texto-base, a água aquecida sobe naturalmente para o reservatório, devido à diferença de densidade (a água quente é menos densa e sobe). Esse processo é chamado de convecção.
Alternativa: E
QUESTÃO 127
As autoridades sanitárias brasileiras têm se preocupado muito nos últimos anos com o aumento da ocorrência de doenças transmitidas por mosquitos, principalmente arboviroses como chikungunya e zika, que se tornaram epidêmicas ou endêmicas em áreas urbanas. Parte de uma análise da relação entre a urbanização e a incidência dessas doenças está representada no fluxograma.
ALMEIDA, L. S.; COTA, A. L. S.; RODRIGUES, D. F. Saneamento, arboviroses e determinantes ambientais: impactos na saúde urbana.
Ciência & Saúde Coletiva, v. 25, n. 10, 2020 (adaptado)
Nesse contexto, como a urbanização está causando riscos à saúde humana?
(A) Disseminando verminoses.
(B) Causando a eutrofização de lagoas.
(C) Aumentando a chance de contato com coliformes.
(D) Diminuindo a população de predadores aquáticos.
(E) Aproximando as pessoas das áreas de ocorrência de mosquitos.
Resolução:
A urbanização pode atuar na redução da biodiversidade aquática de diversas maneiras, como pela contaminação da água, que pode levar à redução dos predadores naturais e, consequentemente, ao aumento de vetores e outros transmissores de doenças aos seres humanos.
Alternativa: D
QUESTÃO 128
Impactos do microplástico
A ação de fatores abióticos aliada à biodeterioração contribuem para a formação de microplásticos, os quais se aderem a outros poluentes orgânicos apolares persistentes, como os derivados de pesticidas lipossolúveis. Há uma proporcionalidade direta entre a solubilidade desses tipos de poluentes e sua concentração nos tecidos dos organismos expostos a eles.
Disponível em: www.ecycle.com.br. Acesso em: 9 dez. 2021 (adaptado).
Em animais vertebrados, essa associação de poluentes será preferencialmente acumulada no tecido
(A) ósseo.
(B) nervoso.
(C) epitelial.
(D) adiposo.
(E) sanguíneo.
Resolução:
Os pesticidas lipossolúveis tendem a se acumular em tecidos ricos em lipídios. O tecido humano com maior quantidade dessa substância orgânica é o tecido adiposo, no qual o organismo humano armazena gordura como reserva energética.
Alternativa: D
QUESTÃO 129
Em aeroportos, por razões de segurança, os passageiros devem ter suas bagagens de mão examinadas antes do embarque, passando-as em esteiras para sua inspeção por aparelhos de raios X. Nessas inspeções, os passageiros são orientados a retirar seus computadores portáteis (notebooks ou laptops) de malas, mochilas ou bolsas para passá-los isoladamente pela esteira.
Que explicação física justifica esse procedimento?
(A) Os raios X não interagem com os componentes metálicos do computador, o que impede a formação de imagens.
(B) Os raios X desmagnetizam o disco rígido do computador, quando refratados pelos componentes metálicos das bagagens de mão.
(C) Os raios X aquecem os materiais metálicos encontrados em bagagens de mão, quando refletidos pelos componentes do computador.
(D) Os raios X não atravessam os componentes densos do computador, o que impede a visualização de objetos que estão à frente ou atrás deles.
(E) Os raios X ionizam os materiais metálicos normalmente encontrados em bagagens de mão, quando difratados pelos componentes do computador.
Resolução:
Os computadores portáteis, como notebooks e tablets, precisam ser retirados das malas nos controles de segurança dos aeroportos e colocados em uma bandeja separada no raio-X. Isso é necessário porque o interior dos computadores e de outros dispositivos eletrônicos pode bloquear ou dificultar a leitura do conteúdo ao redor deles. Se eles ficarem na mala, é mais difícil para o operador do raio-X ver com clareza o que está dentro dela.
A estrutura e os componentes eletrônicos podem criar zonas onde o raio-X não alcança, dificultando a inspeção dos demais objetos e ocultando eventuais itens proibidos ou suspeitos. Além disso, a retirada dos dispositivos eletrônicos também é uma medida de segurança.
Alternativa: D
QUESTÃO 130
Com base em testes realizados em ratos, concluiu-se que os componentes nitrosos são substâncias mutagênicas, ou seja, produzem mutações nas células e possivelmente câncer. Esses compostos podem ser obtidos pela reação entre o nitrito de sódio, que é um conservante adicionado às carnes, e o ácido clorídrico. O ácido nitroso produzido irá reagir com compostos nitrogenados, como as aminas, dando origem aos compostos nitrosos.
Em qual órgão esse processo será iniciado?
(A) Rim.
(B) Fígado.
(C) Intestino.
(D) Pâncreas.
(E) Estômago.
Resolução:
O estômago contém glândulas gástricas que produzem e secretam ácido clorídrico (HC calligraphic l), o qual reage com o nitrato de sódio presente nas carnes ingeridas.
Alternativa: E
QUESTÃO 131
Sistemas agroflorestais (SAFs)
Os sistemas agroflorestais alinham os interesses econômicos aos ecológicos. Esses sistemas podem ser usados na recuperação ambiental de áreas degradadas que se tornaram pouco produtivas, como as utilizadas por muito tempo para pastagem. Para isso, num primeiro momento, as árvores nativas são plantadas em conjunto com culturas agrícolas anuais, como feijão, mandioca, milho e abóbora, que geram renda para os proprietários da terra e incentivam a manutenção do sistema. Em um segundo momento, são introduzidas outras espécies, como trepadeiras e arbustos, de acordo com um arranjo espacial e temporal preestabelecido. Nesse processo, ocorrerão mudanças graduais na estrutura e composição das comunidades vegetais ao longo do tempo, que culminarão no aumento da diversidade do ambiente.
Disponível em: www.embrapa.br. Acesso em: 9 dez. 2021 (adaptado).
O conjunto dessas mudanças graduais é análogo ao processo natural denominado
(A) rotação de culturas.
(B) sucessão ecológica.
(C) coevolução específica.
(D) adaptação por seleção.
(E) convergência adaptativa.
Resolução:
O processo natural de alteração na composição da comunidade ao longo do tempo é denominado sucessão ecológica, análogo ao que ocorreu na situação apresentada pelo texto envolvendo sistemas agroflorestais.
Alternativa: B
QUESTÃO 132
As fibras musculares esqueléticas não são todas iguais. As fibras lentas, também conhecidas como fibras vermelhas, apresentam muitas mitocôndrias e são bem supridas por vasos sanguíneos. Já a fibras rápidas, ou fibras brancas, apresentam poucas mitocôndrias e recebem menor suprimento sanguíneo. Dessa forma, a distribuição das fibras nos músculos esqueléticos do corpo auxilia de forma diferenciada no desempenho físico de um atleta.
SADAVA, D et al. Vida: a ciência da biologia - Volume III: plantas e animais. Porto Alegre: Artmed, 2009 (adaptado).
Um atleta que sonha em disputar os Jogos Olímpicos e tem uma maior proporção de fibras brancas que fibras vermelhas teria mais vantagens na realização da prova de:
(A) Triatlo.
(B) Salto em altura.
(C) Marcha atlética.
(D) Maratona aquática.
(E) Ciclismo em estrada.
Resolução:
As fibras musculares brancas (tipo II) apresentam contração rápida, possuem baixa concentração de mioglobina e mitocôndrias. Nessas células, a obtenção de ATP ocorre predominantemente de forma anaeróbica, sendo mais eficiente para realizar atividades intensas de curta duração, como saltos.
Alternativa: B
QUESTÃO 133
O Cerrado e a Amazônia abrigam grande número de serpentes popularmente conhecidas como cobras-corais. Na Amazônia predominam as corais-verdadeiras, que são peçonhentas, enquanto no Cerrado prevalecem as falsas-corais, que não possuem peçonha. Essas espécies apresentam um padrão de coloração muito semelhante. Essa similaridade traz uma vantagem tanto para as corais falsas como para as verdadeiras.
FRANÇA, F. G. R. [...] serpentes corais em ambientes campestres, savânicos e florestais da América do Sul. Brasília: UnB, 2008 (adaptado).
Nas fotografias, são apresentados exemplos dessas serpentes: uma coral-verdadeira e uma falsa-coral.
SILVA, L. C.; COTTA, G. A.; RESENDE, F. C. Cobra-coral: aplicativo educativo para reconhecimento das cobras-corais do estado de Minas Gerais, Brasil. Herpetologia Brasileira, n. 1, 2021 (adaptado).
Qual é a vantagem dessa similaridade para as falsas-corais?
(A) Facilita a captura de presas.
(B) Diminui a competição por recursos.
(C) Possibilita a geração de indivíduos híbridos.
(D) Reduz a possibilidade de sofrerem predação.
(E) Otimiza o encontro de parceiros reprodutivos.
Resolução:
A falsa-coral, não peçonhenta, é muito semelhante à coral-verdadeira, peçonhenta. Possíveis predadores da falsa-coral evitam essa serpente devido à sua semelhança com a coral-verdadeira, processo descrito como mimetismo batesiano.
Alternativa: D
QUESTÃO 134
O exoesqueleto dos crustáceos é formado por quitina e impregnações de sais calcários e, por isso, é mais duro quando comparado com o exoesqueleto de outros artrópodes. Esse revestimento externo confere proteção, mas, por ser duro, limita o crescimento desses animais.
Para superar essa limitação, o exoesqueleto deve ser
(A) formado somente na fase adulta do animal.
(B) fragmentado para expansão nas áreas de articulação.
´(C) modelado continuamente para ajuste ao tamanho do corpo.
(D) substituído por meio de mudas que ocorrem periodicamente.
(E) impregnado por pequena quantidade de sais para sua distensão.
Resolução:
Por ser rígido e envolver todo o corpo dos artrópodes, o exoesqueleto impede o crescimento do animal. Dessa forma, o crescimento de um artrópode depende da troca do exoesqueleto pequeno por um novo e maior. Esse processo de troca periódica do exoesqueleto é chamado de muda ou ecdise. Em decorrência das mudas, o crescimento dos artrópodes é descontínuo, pois são observados períodos de crescimento rápido alternados com períodos sem crescimento.
Alternativa: D
QUESTÃO 135
Um dos exemplos mais conhecidos de herança recessiva ligada ao cromossomo X é o daltonismo. Como em qualquer distúrbio recessivo ligado ao cromossomo X, existem muito mais homens apresentando o fenótipo com esse tipo de daltonismo do que mulheres. Um casal formado por um homem não daltônico e por uma mulher gestante também não daltônica, mas portadora do gene recessivo para esse tipo de daltonismo, está esperando um bebê. Em uma das consultas de pré-natal, o casal recebeu um heredograma que contém todas as possibilidades de genótipo para esse bebê.
Considere a legenda:
Qual heredograma foi recebido pelo casal?
(A)
(B)
(C)
(D)
(E)
Resolução:
A partir da leitura do enunciado é possível identificar que os indivíduos em questão são portadores dos seguintes genótipos:
Homem não daltônico -XDY
Mulher não daltônica portadora do gene para o daltonismo - XDYd
A partir do cruzamento desse casal, observado no quadro de Punnett, tem-se como possibilidades de descendentes:
Uma mulher não daltônica (XDXD) O
Uma mulher heterozigota portadora do gene para daltonismo
Um homem não daltônico
Um homem daltônico
Sendo assim, a partir da legenda fornecida pela questão, o heredograma recebido pelo casal seria:
Alternativa: B
QUESTÃO 136
Uma empresa produz mochilas escolares sob encomenda. Essa empresa tem um custo total de produção, composto por um custo fixo, que não depende do número de mochilas, mais um custo variável, que é proporcional ao número de mochilas produzidas. O custo total cresce de forma linear, e a tabela apresenta esse custo para três quantidades de mochilas produzidas.
O custo total, em real, para a produção de 80 mochilas será
(A) 2 400,00.
(B) 2 520,00.
(C) 2 550,00.
(D) 2 700,00.
(E) 2 800,00.
Resolução:
Seja o custo fixo K, e seja x o custo variável:
Resolvendo o sistema, tem-se: X = 30 reais por mochila, e k = 150 reais.
Logo, para a produção de 80 mochilas, o custo será
C = 150 + 30 . 80 = 2550 reais.
Alternativa:
QUESTÃO 137
A umidade relativa do ar é um dos indicadores utilizados na meteorologia para fazer previsões sobre o clima. O quadro apresenta as médias mensais, em porcentagem, da umidade relativa do ar em um período de seis meses consecutivos em uma cidade.
Meses Maio Jun. Jul. Ago. Set. Out.
Média mensal da umidade relativa do ar (%) 66 64 54 46 60 64
Nessa cidade, a mediana desses dados, em porcentagem, da umidade relativa do ar no período considerado foi
(A) 56.
(B) 58.
(C) 59.
(D) 60.
(E) 62.
Resolução:
Organizando os dados em rol (ordem crescente, no caso), tem-se: 46, 54, 60, 64, 64, 66.
Mediana = 60 + 62
2
Mediana = 62
Alternativa: E
QUESTÃO 138
Uma empresa de engenheira foi contratada para realizar um serviço no valor de R$ 71 250,00. Os sócios da empresa decidiram que 40% desse valor seria destinado ao pagamento de três engenheiros que gerenciaram o serviço. O pagamento para cada um deles será feito de forma diretamente proporcional ao total de horas trabalhadas. O número de dias e o número de horas diárias trabalhadas pelos engenheiros foram, respectivamente:
engenheiro I: 4 dias, numa jornada de 5 horas e meia por dia;
engenheiro II: 5 dias, numa jornada de 4 horas por dia;
engenheiro III: 6 dias, numa jornada de 2 horas e meia por dia.
Qual a maior diferença, em real, entre os valores recebidos por esse serviço entre dois desses engenheiros?
(A) 1 000
(B) 1 500
(C) 3 500
(D) 3 800
(E) 5 250
Resolução:
Para calcular o valor que seria destinado ao pagamento de três engenheiros, tem-se:
40 = 71250 = 28500
100
Para calcular a quantidade de horas trabalhadas por cada engenheiro:
Engenheiro 1:
4 . 5,5 = 22h
Total de horas E1:
Engenheiro 2:
Total de horas E2: 5. 4 = 20h
Engenheiro 3:
Total de horas E3: 6 . 2,5 = 15h
Seguindo a proporção do texto, encontra-se a constante procurada:
E1 = E2 = E3 = E1 + E2 + E3 = 28500 = 500
22 20 15 22 + 20 + 15 57
Para encontrar o valor que deve ser pago a cada engenheiro, precisamos multiplicar a constante encontrada pelo número de horas trabalhadas. Assim, obtém-se:
Valor recebido pelo Engenheiro 1:
E1 = 500 . 22 = 11000
Valor recebido pelo Engenheiro 2:
E2 = 500 . 200 = 10000
Valor recebido pelo Engenheiro 3:
E3 = 500 . 15 = 7500
Subtraindo do maior valor o menor, tem-se:
11000 – 7500 = 3500
Alternativa: C
QUESTÃO 139
Um hospital tem 7 médicos cardiologistas e 6 médicos neurologistas em seu quadro de funcionários. Para executar determinada atividade, a direção desse hospital formará uma grande equipe com 5 médicos, sendo, pelo menos, 3 cardiologistas.
A expressão numérica que representa o número máximo de maneiras distintas de formar essa equipe é
Resolução:
Ao todo são 7 cardiologistas e 6 neurologistas. Os grupos possíveis são compostos por 3 cardiologistas e 2 neurologistas, ou 4 cardiologistas e 1 neurologista, ou, por fim, 5 cardiologistas.
As combinações são dadas por:
Alternativa: E
QUESTÃO 140
Para melhorar o fluxo de ônibus em uma avenida que tem dois semáforos, a prefeitura reduzirá o tempo em que cada sinal ficará vermelho, que atualmente é de 15 segundos a cada 60 segundos. Admita que o instante de chegada de um ônibus a cada semáforo é aleatório.
O engenheiro de tráfego da prefeitura calculou a probabilidade de um ônibus encontrar cada um deles vermelho, obtendo 15/60. A partir daí, estabeleceu uma mesma redução na quantidade do tempo, em segundo, em que cada sinal ficará vermelho, de maneira que a probabilidade de um ônibus encontrar ambos os sinais vermelhos numa mesma viagem é igual a 4/100, considerando os eventos independentes.
Para isso, a redução do tempo em que o sinal ficará vermelho, em segundo, estabelecida pelo engenheiro foi de
(A) 1,35.
(B) 3,00.
(C) 9,00.
(D) 12,60.
(E) 13,80.
Resolução:
Como os eventos são independentes, tem-se:
x . x = 4
60 60 100
x2 = 144
x =√144
x = 12
Assim, a redução do tempo em que o sinal ficará vermelho, em segundo, estabelecida pelo engenheiro foi de: 15 – 12 = 3 s.
Alternativa: B
QUESTÃO 141
A densidade demográfica de uma região é definida como sendo a razão entre o número de habitantes dessa região e sua área, expressa na unidade habitantes por quilômetro quadrado.
Uma região R é subdividida em várias outras, sendo uma delas a região Q. A área de Q é igual a três quartos da área de R, e o número de habitantes de Q é igual à metade do número de habitantes de R. As densidades demográficas correspondentes a essas regiões são denotadas por d(Q) e d(R).
A expressão que relaciona d(Q) e d(R) é
(A) d(Q) = 1/4 d(R)
(B) d(Q) = 1/2 d(R)
(C) d(Q) = 3/4 d(R)
(D) d(Q) = 3/2 d(R)
(E) d(Q) = 2/3 d(R)
Resolução:
Pelo enunciado, tem-se:
A(Q) = 3/4A(R)
H(Q) = 3/4 A(R)
Assim, as densidades são dadas por:
d(R) = H(R)
A(R)
d(R) = H(Q) = 1/2H(R) = 2 H(R) = 2 . d(R)
A(Q) 3/4A(R) 3 A(R) 3
Alternativa: E
QUESTÃO 142
Atualmente, há telefones celulares com telas de diversos tamanhos e em formatos retangulares. Alguns deles apresentam telas medindo 3 . 1/3 polegadas, com determinadas especificações técnicas. Além disso, em muitos modelos, com a inclusão de novas funções no celular, suas telas ficaram maiores, sendo muito comum encontrarmos atualmente telas medindo 4 .5/6 polegadas, conforme a figura.
A diferença de tamanho, em valor absoluto, entre as medidas, em polegada, das telas do celular 2 e do celular 1, representada apenas com uma casa decimal, é
(A) 0,1.
(B) 0,5.
(C) 1,0.
(D) 1,3.
(E) 1,8.
Resolução:
Pelo enunciado, tem-se:
3 . 1 = 3 + 1 = 7 = 3,5
2 2 2
4 . 5 = 4 + 5 = 29 = 4,838....
6 6 6
Logo, a diferença de tamanho, considerando apenas uma casa decimal, é: 4,8 – 3,5 = 1,3.
Alternativa:
QUESTÃO 143
Uma imobiliária iniciou uma campanha de divulgação para promover a venda de apartamentos que podem ser pagos em 100 parcelas mensais. O valor da primeira delas é fixado no momento da compra, com o pagamento dessa primeira parcela. A partir da segunda parcela, o valor é determinado pela aplicação de um acréscimo percentual fixo ao valor da parcela anterior. Como atrativo, a imobiliária fará o pagamento de todas as parcelas correspondentes ao mês de aniversário do comprador.
Um cliente, que faz aniversário no mês de maio, decidiu comprar um desses apartamentos por meio do financiamento oferecido pela imobiliária, e pretende escolher o mês mais adequado para realizar essa compra, de modo que o valor total dos pagamentos seja o menor possível.
Qual é o mês que esse cliente deverá escolher para realizar a compra do apartamento?
(A) Fevereiro.
(B) Abril.
(C) Maio.
(D) Junho.
(E) Agosto.
Resolução:
Como o valor das parcelas cresce com o tempo, para pagar o menor valor total possível, a última parcela deve cair no mês de maio.
As 100 parcelas correspondem a 100/12 = 8 anos e 4 meses. Assim, nesses 8 anos (ciclos) completos, o primeiro mês deve ser junho e o último mês deve ser maio. Adquirindo o apartamento 4 meses antes de junho, ou seja, em fevereiro, o comprador tem o menor valor total possível.
Alternativa: A
QUESTÃO 144
Um sistema de polias circulares e correias é um dos mecanismos responsáveis pela transmissão de movimento em máquinas rotativas. O manual de um motor traz uma figura representando um sistema composto por duas polias e uma correia de transmissão, tensionada e perfeitamente ajustada sobre as polias, de modo a não apresentar folgas nos contatos com as polias. Considere que as partes dessa correia que não ficam em contato com as polias são representadas por segmentos de reta tangentes às polias.
Para substituição dessa correia, é necessária a especificação de seu comprimento.
Considere 3 como valor aproximado para straight pi π.
A medida do comprimento dessa correia, em centímetro, é
(A) 54.
(B) 60.
(C) 66.
(D) 68.
(E) 72.
Resolução:
Como os segmentos CE e CD tangenciam as duas polias, temos AC // BE e AD // BF Assim, o menor arco assim EF = 1500º
e o maior mede 360º – 150º = 210º
Adotando π = 3, o comprimento do menor arco 150º . 2 . 3 . 4 = 10 cm e o do maior arco EF = 210º . 2 . 3 . 8 = 28 cm
360º 360º
Dessa forma, o comprimento da correia é: 15 + 15 + 10 + 28 = 63
Alternativa: D
QUESTÃO 145
A prefeitura de uma cidade planeja construir três postos de saúde. Esses postos devem ser construídos em locais equidistantes entre si e de forma que as distâncias desses três postos ao hospital dessa cidade sejam iguais. Foram conseguidos três locais para a construção dos postos de saúde que apresentam as características desejadas, e que distam 10 km entre si, conforme o esquema, no qual o ponto H representa o local onde está construído o hospital; os pontos P1, P2 e P3, os postos de saúde; e esses quatro pontos estão em um mesmo plano.
A distância, em quilômetro, entre o hospital e cada um dos postos de saúde, é um valor entre
(A) 2 e 3.
(B) 4 e 5.
(C) 5 e 6.
(D) 7 e 8.
(E) 8 e 9.
Resolução:
As distâncias entre os postos são iguais e os pontos formam um triângulo equilátero de 10 km em cada lado. O hospital é equidistante dos postos e corresponde aos pontos notáveis do triângulo (baricentro, ortocentro, incentro e circuncentro). Dessa maneira, prolongando o segmento HP1, encontra-se o ponto M, que divide o lado P2P3 em duas partes iguais, formando um ângulo de 90°.
A partir do triângulo MHP2, tem-se:
cos 30º = 5
HP2
√3 = 5
2 HP2
HP2 = 10 = 10 . √3 = 10 . 1,7 = 5,6
√3 3 3
A distância entre o hospital e os postos está entre 5 e 6 km.
Alternativa: C
QUESTÃO 146
Projetistas de uma fábrica de amortecedores realizaram uma série de experimentos que produziram oscilações semelhantes ao comportamento do gráfico de uma senoide, para qualquer tipo de estrada. Cada experimento teve duração de 20 minutos, sendo os 9 primeiros minutos em superfície que simula uma rodovia asfaltada, e os 11 minutos restantes em superfície que simula uma estrada de chão.
Para os amortecedores serem aprovados no experimento, exige-se que as amplitudes das ondas oscilatórias, em cada tipo de superfície, sejam constantes e, ainda, que a amplitude da oscilação do amortecedor no asfalto seja menor do que sua amplitude da oscilação na estrada de chão.
O tipo de gráfico que descreve o comportamento oscilatório de um amortecedor aprovado nesse experimento é
(A)
(B)
(C)
(D)
(E)
Resolução:
Nos primeiros 9 minutos, a amplitude do gráfico deve ser menor do que nos 11 minutos finais. Como essas amplitudes devem permanecer constantes nesses intervalos, a única alternativa que corresponde a essas restrições é a A.
Alternativa: A
QUESTÃO 147
Um jardineiro dispõe de k metros lineares de cerca baixa para fazer um jardim ornamental. O jardim, delimitado por essa cerca, deve ter a forma de um triângulo equilátero, um quadrado ou um hexágono regular. A escolha será pela forma que resulte na maior área. O jardineiro escolherá a forma de
(A) hexágono regular, pois a área do jardim, em metro quadrado, k2√3
24
(B) hexágono regular, pois a área do jardim, em metro quadrado, será 3k2√3
2
(C) quadrado, pois a área do jardim, em metro quadrado, k2
16
(D) triângulo equilátero, pois a área do jardim, em metro quadrado, será k2√3
36
(E) triângulo equilátero, pois a área do jardim, em metro quadrado, será k2√3
4
Resolução:
Um jardineiro dispõe de k metros de cerca para fazer um jardim ornamental. Caso o jardineiro faça um: triângulo equilátero, cada lado terá medida k/3 assim, sua área será:
quadrado, cada lado terá medida straight k/4, assim, sua área será:
hexágono regular, cada lado terá medida straight k/6, assim, sua área será:
Considerando que √3 = 1,73, percebe-se que:
Portanto, A3, A2 , A1,
ou seja, o jardineiro deve construir um jardim ornamental no formato de um hexágono regular, cuja área é, em metros quadrados, k2√3
24
Alternativa: A
QUESTÃO 148
Um aeroporto disponibiliza o serviço de transporte gratuito entre seus dois terminais utilizando os ônibus A e B, que partem simultaneamente, de hora em hora, de terminais diferentes. A distância entre os terminais é de 9 000 metros, e o percurso total dos ônibus, de um terminal ao outro, é monitorado por um sistema de cinco câmeras que cobrem diferentes partes do trecho, conforme o esquema.
O alcance de cada uma das cinco câmeras é:
câmera I: 1/5;
câmera II: 3/10 do percurso;
câmera III: 1/10 do percurso;
câmera IV:1/10do percurso;
câmera V: 3/10 do percurso.
Em determinado horário, o ônibus A parte do terminal 1 e realiza o percurso total com velocidade constante de 250 space straight m divided by min; enquanto o ônibus B, que parte do terminal 2, realiza o percurso total com velocidade constante de 150 space straight m divided by min.
Qual câmera registra o momento em que os ônibus A e B se encontram?
(A) I
(B) II
(C) iii
(D) IV
(E) V
Resolução:
velocidade média é dada por
em que increment straight s é a variação de posição e increment straight t é a variação de tempo.
Partindo do Terminal 1, se o ônibus A percorreu uma distância x, então, o ônibus B terá percorrido uma distância 9000 - x
e
Para que os ônibus A e B se encontrem, o tempo percorrido por eles deve ser o mesmo, já que eles partem do mesmo instante, ou seja:
Observe abaixo o registro de cada uma das câmeras, partindo do Terminal 1:
Câmera I: 0 m a 1 800 m.
Câmera II: 1 800 m a 4 500 m.
Câmera III: 4 500 m a 5 400 m.
Câmera IV: 5 400 m a 6 300 m.
Câmera V: 6 300 m a 9 000 m.
Como os ônibus se encontraram a 5 625 metros do Terminal 1, a câmera que registrou esse encontro foi a Câmera IV.
Alternativa: D
QUESTÃO 149
A criptografia refere-se à construção e análise de protocolos que impedem terceiros de lerem mensagens privadas. Júlio César, imperador romano, utilizava um código para proteger as mensagens enviadas a seus generais. Assim, se a mensagem caísse em mãos inimigas, a informação não poderia ser compreendida. Nesse código, cada letra do alfabeto era substituída pela letra três posições à frente, ou seja, o "A" era substituído pelo "D", o "B" pelo "E", o "C" pelo "F", e assim sucessivamente.
Disponível em: www.codifica.ibict.br. Acesso em: 15 out. 2019.
Qualquer código que tenha um padrão de substituição de letras como o descrito é considerado uma Cifra de César ou um Código de César. Note que, para decifrar uma Cifra de César, basta descobrir por qual letra o "A" foi substituído, pois isso define todas as demais substituições a serem feitas.
Uma mensagem, em um alfabeto de 26 letras, foi codificada usando uma Cifra de César. Considere a probabilidade de se descobrir, aleatoriamente, o padrão utilizado nessa codificação, e que uma tentativa frustrada deverá ser eliminada nas tentativas seguintes.
A probabilidade de se descobrir o padrão dessa Cifra de César apenas na terceira tentativa é dada por
(A)
(B)
(C)
(D)
(E)
Resolução:
Para que o padrão seja descoberto apenas na terceira tentativa, é possivel observar:
1ª tentativa: A pessoa deseja encontrar a letra A, mas erra. Como ela acerta apenas na 3ª tentativa, restam apenas 25 possibilidades. Dentre estas 25 possibilidades, uma seria a correta e outras 24, incorretas. Como a pessoa errou, a probabilidade é dada por
2ª tentativa: Novamente a pessoa deseja encontrar a letra A, mas erra. Como ela acerta apenas na 3ª tentativa, restam apenas 24 possibilidades, já que a tentativa frustrada anteriormente foi descartada. Dentre estas 24 possibilidades, uma seria a correta e outras 23 incorretas. Como a pessoa errou, a probabilidade é dada por
3ª tentativa: Descartadas as 2 possibilidades frustradas, restaram apenas 23 possibilidades e, como agora a pessoa acertou, a probabilidade é dada por
Portanto, a probabilidade de a pessoa decifrar o Código de César apenas na 3ª tentativa é
Alternativa: E
QUESTÃO 150
Em uma região com grande incidência de terremotos, observou-se que dois terremotos ocorridos apresentaram magnitudes M1 e M2, medidos segundo a escala Richter, e liberaram energias iguais a E1 e E2, respectivamente. Entre os estudiosos do assunto, é conhecida uma expressão algébrica relacionando esses valores dada por
Estudos mais abrangentes observaram que o primeiro terremoto apresentou a magnitude M1 = 6,9 e a energia liberada foi um décimo da observada no segundo terremoto.
O valor aproximado da magnitude M2 do segundo terremoto, expresso com uma casa decimal, é igual a
(A) 5,4.
(B) 6,2.
(C) 7,6.
(D) 8,2.
(E) 8,4.
Resolução:
Substituindo as energias liberadas pelos terremotos na fórmula fornecida, tem-se:
Alternativa: C
QUESTÃO 151
Uma indústria faz uma parceria com uma distribuidora de sucos para lançar no mercado dois tipos de embalagens. Para a fabricação dessas embalagens, a indústria dispõe de folhas de alumínio retangulares, de dimensões 10 cm por 20 cm. Cada uma dessas folhas é utilizada para formar a superfície lateral da embalagem, em formato de cilindro circular reto, que posteriormente recebe fundo e tampa circulares. A figura ilustra, dependendo de qual das duas extensões será utilizada como altura, as duas opções para formar a possível embalagem
Dentre essas duas embalagens, a de maior capacidade apresentará volume, em centímetro cúbico, igual a
(A) 4000π
(B) 2000π
(C) 4000
π
(D) 1000
π
(E) 500
π
Resolução:
A embalagem 1 tem altura de 20 cm e comprimento da circunferência da base medindo 10 cm.
Então, seu volume será:
A embalagem 2 tem altura de 10 cm e comprimento da circunferência da base medindo 20 cm.
Então, seu volume será:
A embalagem de maior volume é a 2, com volume, em centímetro cúbico, igual a
Alternativa: D
QUESTÃO 152
As receitas anuais obtidas por uma indústria no período de 2014 a 2021, em milhão de reais, foram registradas, por pontos, em um gráfico. Nele, também está representada a reta que descreve a tendência de evolução das receitas. Essa reta pode ser utilizada para estimar as receitas dos anos seguintes.
A estimativa da receita, em milhão de reais, dessa indústria, para o ano de 2026, obtida a partir dessa reta de tendência, é
(A) 7.
(B) 8.
(C) 9.
(D) 10.
(E) 11.
Resolução:
Como o gráfico é representado por uma reta, pode-se concluir que a função que representa o gráfico é da forma f(x) + ax + b, onde f(x) é a receita em milhões. Assim, substituindo os pontos dados, tem-se:
Substituindo em f(x) = ax + b
Logo,
Por fim, calculando a receita no ano de 2026, segue:
Alternativa: B
QUESTÃO 153
Um tanque, em formato de paralelepípedo reto retângulo, tem em seu interior dois anteparos verticais, fixados na sua base e em duas paredes opostas, sendo perpendiculares a elas, conforme a figura.
Esses anteparos, de espessura desprezíveis, estão instalados de maneira a dividir a base do tanque em três retângulos congruentes, tendo suas alturas iguais à metade e a um quarto da altura do tanque. O tanque é abstecido por uma entrada situada no teto, através de um duto que despeja água a uma vazão constante, sendo necessárias 12 horas para finalizar o seu enchimento.
O gráfico que descreve, em cada instante, a maior altura de coluna de água, dentre aquelas que vão sendo formadas ao longo do enchimento do tanque, é
Esses anteparos, de espessura desprezíveis, estão instalados de maneira a dividir a base do tanque em três retângulos congruentes, tendo suas alturas iguais à metade e a um quarto da altura do tanque. O tanque é abstecido por uma entrada situada no teto, através de um duto que despeja água a uma vazão constante, sendo necessárias 12 horas para finalizar o seu enchimento.
O gráfico que descreve, em cada instante, a maior altura de coluna de água, dentre aquelas que vão sendo formadas ao longo do enchimento do tanque, é
(A)
(B)
(C)
(D)
(E)
Resolução:
Considerando que os anteparos dividem o tanque em três compartimentos, tem-se:
Nas primeiras duas horas
a água enche apenas o primeiro compartimento, e a altura da água tem crescimento linear referente a 1/3 da área da base do paralelepípedo.
Nas próximas quatro horas, a altura máxima da água permanece constante, pois os demais compartimentos estão sendo enchidos.
Ao completar seis horas
, a altura da água será a mesma nos três compartimentos.
Em seguida, o nível da água voltará a subir, tendo um crescimento linear, mas a taxa de crescimento será menor do que nas duas primeiras horas, pois o aumento da altura é inversamente proporcional à área base, e neste momento o acréscimo de altura se refere à área da base total do paralelepípedo, que é maior do que a da primeira etapa.
Alternativa: B
QUESTÃO 154
Contratos de vários serviços disponíveis na internet apresentam uma quantidade excessiva de informações. Isso faz com que o tempo necessário para a leitura desses contratos possa ser longo.
O quadro apresenta uma amostra do tempo considerado necessário para a leitura completa do contrato de alguns serviços digitais.
ROMERO, L. Não li e concordo. Superinteressante,
- 307, ago. 2012 (adaptado).
O tempo médio, em minuto, necessário para a leitura completa de um contrato de serviço dentre os listados no quadro é, com uma casa decimal, aproximadamente,
(A) 13,0.
(B) 15,0.
(C) 19,8.
(D0 20,0.
(E) 23,3.
Resolução:
O tempo médio é dado pela média aritmética simples dos tempos necessários. Dessa forma, tem-se:
Alternativa: C
QUESTÃO 155
Um proprietário pretende instalar um sensor de presença para a proteção de seu imóvel. O sensor deverá detectar movimentos de objetos e pessoas numa determinada região plana. A figura ilustra a vista superior da área de cobertura (setor circular em azul) de um sensor colocado no ponto S. Essa área depende da medida do ângulo straight alpha, em grau, e do raio R, em metro.
Ao aumentar o ângulo straight alpha ou o raio R aumenta-se a área de cobertura do sensor. Entretanto, quanto maior essa área, maior o preço do sensor.
Para esse fim, há cinco tipos de sensores disponíveis no mercado, cada um com as seguintes características:
1ipo I: 15º R = 20 m;
tipo II: 30º e R = 22 m;
tipo III: 40º e R = 12 m;
tipo IV: 60º e R = 16 m;
tipo V: 90º e R = 10 m.
Esse proprietário pretende adquirir um desses sensores que seja capaz de cobrir, no mínimo, uma área de medida 70 m2, com o menor preço possível.
Use 3 como valor aproximado para π.
O proprietário do imóvel deverá adquirir o sensor do tipo
(A) I.
(B) II.
(C) III.
(D) IV.
(E) V.
Resolução:
Tipo I:
Tipo II:
Tipo III:
Tipo IV:
Tipo IV:
Os tipos II, IV e V cobrem áreas superiores a 70 m2, mas o sensor do tipo V tem menor preço.
Alternativa: E
QUESTÃO 156
O uso de aplicativos de transporte tem sido uma alternativa à população que busca preços mais competitivos para se locomover, principalmente nas grandes cidades. As formas usadas para determinar o valor cobrado por cada viagem variam de um aplicativo para outro, mas, em geral, o valor V a ser pago, em real, varia em função de:
tarifa base F: valor fixo, em real, cobrado no início da viagem;
tempo T: tempo, em minuto, de duração da viagem;
distância D: distância percorrida, em quilômetro.
Um desses aplicativos cobra R$ 2,00 de valor fixo, acrescido de R$ 0,26 por minuto de viagem e de R$ 1,40 por quilômetro rodado.
Nessas condições, a expressão que fornece o valor V a ser pago por uma viagem desse aplicativo é
(A) 2,00F + 0,26T + 1,40D
(B) 2,00 + 0,26T + 1,4D
(C) 2,00 + 0,26T + D
(D) 0,26T + 1,40D
(E) F + T + D
Resolução:
O valor V a ser pago é a taxa fixa mais a taxa variada. A taxa variada é composta pelo valor cobrado por minuto e pelo valor cobrado por quilômetro rodado: V = 2,00 + 0,26 . T + 1,40D
Alternativa: B
QUESTÃO 157
Uma piscina tem capacidade de 2 500 000 litros. Seu sistema de abastecimento foi regulado para ter uma vazão constante de 6 000 litros de água por minuto.
O mesmo sistema foi instalado em uma segunda piscina, com capacidade de 2 750 000 litros, e regulado para ter uma vazão, também constante, capaz de enchê-la em um tempo 20% maior que o gasto para encher a primeira piscina.
A vazão do sistema de abastecimento da segunda piscina, em litro por minuto, é
(A) 8 250.
(B) 7 920.
(C) 6 545.
(D) 5 500.
(E) 5 280.
Resolução:
Primeira piscina:
Volume = 2 500 000 L
Vazão = 6 000 L/min
Com isso, o tempo de abastecimento é:
2 500 000 L = 25000 min
6 000 L/min 6
Segunda piscina:
Volume = 2 750 000L
Tempo de abastecimento = 2 500 . 1,2 = 500 min
6
Portanto, a vazão será:
2 750 000 L = 5 500 L/min
500 min
Alternativa: D
QUESTÃO 158
Uma tubulação despeja sempre o mesmo volume de água por unidade de tempo em uma caixa-d'água, o que significa dizer que a vazão de água nessa tubulação é constante. Na junção dessa tubulação com a caixa-d'água, está instalada uma membrana de filtragem cujo objetivo é filtrar eventuais impurezas presentes na água, combinado a um bom fluxo de água. O fluxo (φ) de água através da superfície da membrana é diretamente proporcional à vazão de água na tubulação, medida em mililitro por segundo, e inversamente proporcional à área da superfície da membrana, medida em centímetro quadrado.
A unidade de medida adequada para descrever o fluxo (φ) de água que atravessa a superfície da membrana é
(A) mL . s . cm2
(B) mL . cm2 / s
(C) mL / cm2 . s
(D) cm2 . s / mL
(E) cm2 / mL . s
Resolução:
Pelo texto, tem-se:
Fluxo de água (φ) diretamente proporcional à vazão V (mL/s)
Fluxo de água (φ) Fluxo de água (cm2)
Com isso, obtém-se a seguinte relação:
Portanto, a unidade de medida do fluxo de água é:
Alternativa: C
QUESTÃO 159
m uma loja de defensivos agrícolas, os preços de alguns produtos foram divulgados em um cartaz.
Sabe-se que 1 litro de defensivo do Tipo A é suficiente para aplicação em 0,5 hectare (ha), enquanto que 1 litro de defensivo do Tipo B é suficiente para aplicação em 0,4 ha. Um agricultor precisa comprar, nessa loja, uma quantidade de litros de defensivo suficiente para aplicar em uma área de 20 ha, além de levar uma máscara para aplicação.
O valor mínimo, em real, a ser gasto pelo agricultor é
(A) 147,00.
(B) 150,00.
(C) 162,50.
(D) 165,75.
(E) 168,00.
Resolução:
Custo do agricultor usando o Defensivo Tipo A:
Portanto, na compra do defensivo A, não será necessário o pagamento pela máscara para aplicação.
Custo do agricultor usando o Defensivo Tipo B:
Neste caso, é necessário adquirir a máscara pelo valor de R$ 12,50.
Alternativa: C
QUESTÃO 160
Uma doceira vende e entrega, em seu bairro, porções de 100 g de docinhos de aniversário. Atualmente, a taxa única de entrega é R$ 10,00, e o valor cobrado por uma porção é R$ 25,00. Por uma estratégia de vendas, a partir da próxima semana, a taxa única de entrega será R$ 15,00, e um novo valor será cobrado por uma porção, de maneira que o valor total a ser pago por um cliente na compra de 5 porções permaneça o mesmo.
A partir da próxima semana, qual será o novo valor cobrado, em real, por uma porção?
(A) 12,50
(B) 20,00
(C) 24,00
(D) 30,00
(E) 37,50
Resolução:
Custo atual open (Ci) na compra de cinco porções:
Ci = 10 + 25,5 = 135 reais
Custo na próxima semana (Cf) na compra de cinco porções:
Cf = 15 + x . 5
Logo, para manter o custo, é preciso que:
15 + x . 5 = 135
5x = 120
x = 24 reais por porção
Alternativa: C
QUESTÃO 161
Uma empresa tem 400 funcionários, distribuídos em três setores: administrativo, logística e produção. O gráfico apresenta a distribuição quantitativa desses funcionários, por setor e por faixa etária.
A maior probabilidade é que o funcionário sorteado esteja na faixa etária
(A) entre 25 e 45 anos, pois é a faixa etária com maior quantidade de funcionários.
(B) entre 25 e 45 anos, pois é a única faixa etária cujas porcentagens são maiores do que as porcentagens mínimas de cada setor.
(C) até 25 anos, pois é a única faixa etária cujos percentuais associados aos setores aumentam com o aumento da quantidade de funcionários por setor.
(D) até 25 anos, pois é a faixa etária que apresenta maior quantidade de funcionários no setor de produção, que é o setor que emprega metade dos funcionários dessa empresa.
(E) a partir de 45 anos, pois a soma das porcentagens associadas a essa faixa etária é 110%, que é maior do que as respectivas somas associadas às outras faixas etárias, que são 105% e 85%.
Resolução:
- I) Quantidade de funcionários “até 25 anos”
0,20 . 80 + 0,25 . 125 + 0,40 . 200 = 16 + 30 + 80 = 126
- II) Quantidade de funcionários “entre 25 e 45 anos”:
0,30 . 80 + 0,40 . 120 + 0,35 . 200 = 24+ 48 + 70 = 142
III) Quantidade de funcionários “a partir de 45 anos”:
0,50 . 80 + 0,35 . 120 + 0,25 . 200 = 40 + 42 + 50 = 132
Como dito no enunciado, todos os funcionários terão igual probabilidade de serem sorteados. Assim, a probabilidade é maior para aquele grupo que apresenta a maior quantidade de funcionários, ou seja, a faixa etária “entre 25 e 45 anos”.
A saber, essas probabilidades seriam dadas por:
PI = 126/400 = 31,5%
PII = 142/400 = 31,5%
PIII = 132/400 = 33%
Alternativa: A
QUESTÃO 162
Em um jogo virtual para celular, um personagem pode percorrer trajetórias retilíneas voando ou se deslocando ao longo de paredes. Considere que o personagem descreve a trajetória ABCDEF, em que os pontos A, D e E estão em um plano paralelo ao que contém os pontos B e C, sendo esses dois planos ortogonais ao plano da base que contém o ponto F, conforme a figura.
A projeção ortogonal, sobre o plano da base, da trajetória ABCDEF descrita pelo personagem é
(A)
(B)
(C)
(D)
(E)
Resolução:
Projetando cada um dos pontos ABCDEF no plano da base, tem-se:
Assim, observa-se que a alternativa que condiz com essa projeção é:
Resolução: C
QUESTÃO 163
O tamanho mínimo que a visão humana é capaz de visualizar sem o uso de equipamento auxiliar é equivalente a 100 micrômetros (1 micrômetro = 10 to the power of negative 3 end exponent milímetros). Uma estudante pretende visualizar e analisar hemácias do sangue humano, que medem 0,007 mm de diâmetro. Ela adquiriu um microscópio óptico que tem uma lente ocular que amplia em 10 vezes a imagem do objeto em observação, e um conjunto de lentes objetivas com estas capacidades de ampliação:
lente I: 2 vezes;
lente II: 10 vezes;
lente III: 15 vezes;
lente IV: 1,1 vez;
lente V: 1,4 vez.
O funcionamento desse microscópio permite o uso da lente ocular sozinha ou a combinação dela com uma de suas lentes objetivas, proporcionando, nesse caso, um aumento de sua capacidade de ampliação final, que é dada pelo produto entre as capacidades de ampliação da ocular e da objetiva.
Essa estudante pretende selecionar a lente objetiva de menor capacidade de ampliação que permita, na combinação com a ocular, visualizar hemácias do sangue humano.
A lente objetiva a ser selecionada pela estudante é a
(A) I.
(B) II.
(C) III.
(D) IV.
(E) V.
Resolução:
Pretende-se visualizar hemácias de diâmetro igual a 0,007 mm. Para isso, deve-se multiplicar esse valor pela capacidade de ampliação da lente ocular (a) e da lente objetiva (β), 100 micrômetros = 100 . 10-11 mm).
Assim, tem-se:
0,007 . a . β = 100 . 10-3
0,007 . 10 . β = 0,1
Β = 0,1 = 10 = 1,42857...
0,07 7
Desse modo, a lente objetiva de menor capacidade de aumento que atende a essa necessidade é a lente objetiva I, a qual possui uma capacidade de aumento de 2 vezes.
Alternativa: A
QUESTÃO 164
Ao calcular a média de suas notas em 4 provas, um estudante dividiu, por engano, a soma das notas por 5. Com isso, a média obtida foi 1 unidade menor do que deveria ser, caso fosse calculada corretamente.
O valor correto da média das notas desse estudante é
(A) 4.
(B) 5.
(C) 6.
(D) 19.
(E) 21.
Resolução:
Sejam S e M a soma das notas nas quatro provas e a média correta, respectivamente. Assim:
Alternativa: B
QUESTÃO 165
Para abrir a porta de uma empresa, cada funcionário deve cadastrar uma senha utilizando um teclado alfanumérico como o representado na figura.
Por exemplo: a tecla que contém o número 2 traz as letras correlacionadas A, B e C. Cada toque nessa tecla mostra, sequencialmente, os seguintes caracteres: 2, A, B e C. Para os próximos toques, essa sequência se repete. As demais teclas funcionam da mesma maneira.
As senhas a serem cadastradas pelos funcionários devem conter 5 caracteres, sendo 2 algarismos distintos seguidos de 3 letras diferentes, nessa ordem. Um funcionário irá cadastrar sua primeira senha, podendo escolher entre as teclas que apresentam os números 1, 2, 5, 7 e 0 e as respectivas letras correlacionadas, quando houver.
O número de possibilidades diferentes que esse funcionário tem para cadastrar sua senha é
(A) 11 520.
(B) 14 400.
(C) 18 000.
(D0 312 000.
(E) 390 000.
Resolução:
As teclas disponíveis para o cadastro da senha são 1, 2, 5, 7 e 0, ou seja, 5 possibilidades de números. As únicas teclas que possuem letras são 2, 5 e 7, com 10 letras ao todo.
Desse modo, como a senha deve ser composta por dois números e três letras, sem repetição, há:
5 . 4 . 10 . 9 . 8 = 14 400 possibilidades.
Alternativa: B
QUESTÃO 166
Um artesão utiliza dois tipos de componentes, X e Y, nos enfeites que produz. Ele sempre compra todos os componentes em uma mesma loja. O quadro apresenta os preços dos dois tipos de componentes nas lojas I e II.
Ele confeccionará enfeites formados por duas unidades do componente X e uma unidade do componente Y e efetuará a compra na loja que oferecer o menor valor total para a confecção de um enfeite.
O artesão efetuará a compra na loja
(A) I, pois o valor é R$ 7,00.
(B) I, pois o valor é R$ 4,00.
(C) II, pois o valor é R$ 6,00.
(D) I, pois anuncia o componente com o menor preço.
(E) II, pois o componente X, que é o mais utilizado, tem menor preço.
Resolução:
Em cada enfeite, deverão ser utilizadas duas unidades do componente X e uma unidade do componente Y.
Desse modo, o valor total de confecção de cada enfeite será:
Loja I:
Valor: 2 . 3 + 1 . 1 = 7 reais
Loja II:
Valor: 2 . 2 + 1 . 4 = 8 reais
Portanto, o artesão efetuará a compra na loja I, pois o valor é R$ 7,00 reais.
Alternativa: A
QUESTÃO 167
João e Felipe participaram, na escola, de uma maratona de matemática na qual, durante uma semana, resolveram 200 questões cada. Nessa maratona, a porcentagem P de acertos de cada participante é convertida em um conceito:
insatisfatório: se 0 ≤ P < 50;
regular: se 50 ≤ P < 60;
bom: se 60 ≤ P < 75;
muito bom: se 75 ≤ P < 90;
excelente: se 0 ≤ P ≤ 75.
João acertou 75% das questões da maratona e Felipe acertou 30% a menos que a quantidade de questões que João acertou.
Os conceitos de João e Felipe foram, respectivamente,
(A) muito bom e bom.
(B) muito bom e regular.
(C) muito bom e insatisfatório.
(D) bom e regular.
(E) bom e insatisfatório.
Resolução:
- João acertou 75% das questões, enquadrando-se no conceito "muito bom", pois, pela tabela, esse percentual se enquadra no intervalo 75 ≤ P < 90
- Por outro lado, Felipe se enquadra no intervalo "regular", pois sua porcentagem de acerto corresponde 0,7 . 75 = 52%, isto é, 50 ≤ P < 60
Alternativa: B
QUESTÃO 168
Três grandezas (I, II e III) se relacionam entre si. Os gráficos a seguir, formados por segmentos de reta, descrevem as relações de dependência existentes entre as grandezas I e II, e entre as grandezas II e III.
O valor máximo assumido pela grandeza III, quando a grandeza I varia de 1 a 3, é
(A) 1,0.
(B) 2,5.
(C) 3,0.
(D) 3,5.
(E) 4,0.
Resolução:
- Observando o gráfico 1, pode-se concluir que a grandeza I, variando de 1 a 3, faz com que a grandeza II varie de 1,5 a 3,5.
- Já observando o 2º gráfico, pode-se concluir que, quando a grandeza II assume o valor 1,5, a grandeza III assume o valor 2,5.
III. Observando-se o mesmo gráfico 2, pode-se concluir que, quando a grandeza II assume o valor 3,0, a grandeza III atinge o valor 1.
Analisando as informações obtidas em II e III, pode-se concluir que a grandeza 3 tem seus valores mínimos e máximos entre 1 e 2,5. Assim, pode-se concluir que o valor máximo pedido pelo item é 2,5.
Alternativa: B
QUESTÃO 169
Uma criança, utilizando um aplicativo, escreveu uma mensagem para enviar a um amigo. Essa mensagem foi escrita seguindo estas etapas:
A criança seguiu copiando e colando, em cada etapa, o que tinha no visor na etapa imediatamente anterior, até concluir a 20ª etapa. Em seguida, enviou a mensagem.
Qual foi o total de figuras contidas na mensagem enviada?
(A) 3 . 219
(B) 3 . 220
(C) 3 . 221
(D) 3 . 220 - 1
(E) 3 . 220 - 3
Resolução:
- Pelos dados do texto, conclui-se que a sequência descrita trata-se de uma progressão geométrica com o a1 = 3 e razão q = 2.
- Dessa maneira, para encontrar a vigésima etapa, é necessário determinar o vigésimo termo desta P.G.
Assim, tem-se:
an = a1 . q(n -1)
a20 = a1 . q(20 -1)
a20 = 3 . 2(19)
Alternativa: A
QUESTÃO 170
Um casa de shows terá um evento cujo custo total de produção é de R$ 34 350,00, sendo que comporta 500 pessoas. O preço do ingresso será de R$ 130,00 e, normalmente, 60% das pessoas adquirem meia-entrada, pagando R$ 65,00 pelo ingresso. Além do faturamento proveniente da venda de ingressos, a casa de shows vende, com 60% de lucro, bebidas e petiscos ao público no dia do evento.
Após ter vendido todos os 500 ingressos, constatou-se que a quantidade de meias-entradas vendidas superou em 50% o que estava previsto, impactando o faturamento estimado com a venda de ingressos.
No dia do evento, decidiu-se manter o percentual de 60% de lucro sobre as bebidas e petiscos, pois todo o público que comprou ingresso compareceu ao show. Com isso, espera-se ter lucro de R$ 17 000,00 nesse evento.
Para que se alcance o lucro esperado, o gasto médio por pessoa com bebidas e petiscos, em real, deverá ser de
(A) 19,50.
(B) 28,80.
(C) 34,00.
(D) 52,00.
(E) 68,70.
Resolução:
A partir do texto, tem-se:
Que o custo da festa será de R$ 34 350,00 e que o lucro esperado é de R$ 17 000,00. Logo, é possível calcular a receita esperada, que será:
R = 34 350 + 17 000 = R$ 51 350,00
Para calcular o total arrecadado com a venda de ingressos, é preciso levar em conta que a venda da meia-entrada superou em 50% o valor previsto, que era de 60% das 500 pesosas que o evento comporta.
Quantidade prevista de meia-entrada:
60% de 500 = 0,6 . 500 = 300 pessoas pagando meia.
Porém, como houve um aumento de 50% do número de meias-entradas em relação ao esperado, tem-se que:
50% de 300 = 0,5 times 300 = 150 meias-entradas a mais.
Conclui-se, então, que foram vendidas 300 + 150 = 450 meias-entradas e, consequentemente, 500 - 450 = 50 entradas inteiras.
Como o valor o ingresso é de R$ 130,00, tem-se que o valor I, arrecadado com ingressos, foi de:
I = 450 times 65 + 50 times 130 = R$ 35 750,00
A receita (R) será obtida por meio da venda de ingressos (I) e da venda de bebidas com lucro de 60% (B).
R = I + B
51 350 = 35 750 + B
B = R$ 15 600,00
Como o percentual de lucro foi mantido em 60%, tem-se que 60% do valor arrecadado em bebida deve totalizar R$ 15 600,00.
60% times B = 15 600,00
0,6 times B = 15 600,00
B = R$ 26 000,00
Tendo um número de 500 pessoas comparecendo à festa, o valor gasto por pessoa em bebidas e petiscos deve ser:
26 000 = 52,00 reias
500
Alternativa: D
QUESTÃO 171
Para obter um sólido de revolução (rotação de 360° em torno de um eixo fixo), uma professora realizou as seguintes etapas:
recortou o trapézio retângulo PQRS de um material rígido;
afixou o lado PS do trapézio em uma vareta fixa retilínea (eixo de rotação);
girou o trapézio 360° em torno da vareta e obteve um sólido de revolução.
Observe a figura que apresenta o trapézio afixado na vareta e o sentido de giro.
O sólido obtido foi um(a)
(A) cone.
(B) cilindro.
(C) pirâmide.
(D) tronco de cone.
(E) tronco de pirâmide.
Resolução:
Ao rotacionar um trapézio retângulo em torno de sua altura, coincidente com um lado transversal, encontra-se como resultado um tronco de cone.
Alternativa: D
QUESTÃO 172
estádio do Maracanã passou por algumas modificações estruturais para a realização da Copa do Mundo de 2014, como, por exemplo, as dimensões do campo retangular. se adaptar aos padrões da Fifa, as dimensões do campo foram reduzidas de110 m x 75m para 105 x 68.
Disponível em: http://virgula.uol.com.br. Acesso em 14 ago. 2013 (adaptado).
Em quantos metros quadrados a área do campo do Maracanã foi reduzida?
(A) 24
(B) 35
(C) 555
(D) 1 110
(E) 1 145
Resolução:
O valor da área antes da reforma é dado por 110 m x 75m = 8250m2. Após a reforma, a área do campo passou a ser 105 m x 68 m 7149m2
Fazendo 8250m2 - 7149m2 = 1110m2
Alternativa: D
QUESTÃO 173
Uma sala com piso no formato retangular, com lados de medidas 3 m e 6 m, será dividida em dois ambientes. Para isso, serão utilizadas colunas em formato cilíndrico, dispostas perpendicularmente ao piso e representadas na figura pelos círculos de cor azul. Os centros desses círculos estarão sobre uma reta paralela aos lados de menor medida do piso da sala. Os vãos entre duas colunas e entre uma coluna e a parede não poderão ser superiores a 15 cm.
Para efetuar a compra dessas colunas, foram feitos orçamentos com base em dados fornecidos por cinco lojas.
A compra será realizada na loja cujo orçamento resulte no menor valor total possível.
A compra será realizada na loja
(A) I.
(B) II.
(C) III.
(D) IV.
(E) V.
Resolução:
Para determinar a quantidade de pilares, pode-se somar a distância de 15 cm (máxima entre as paredes e os pilares) com o diâmetro de cada circunferência. Divide-se, então, a largura de 3 m (300 cm) por esse valor a fim de determinar a quantidade de pilares necessários, arredondando o valor para cima, no caso de um resultado decimal. Assim,
- I) 15 cm + 10 cm = 25 cm
300 = 12
25
Como o custo de cada pilar é R$ 60,00, o custo total é de 12 x R$ 60,00 = R$ 720,00.
- II) 15 cm + 20 cm = 35 cm
300 = 8,57
35
Considerando 9, o custo será de 9 x R$ 70,00 = R$ 630,00.
III) 15 cm + 24 cm = 39 cm
300 = 7,69
39
Considerando 8, o custo será de 8 x R$ 75,00 = R$ 600,00.
- IV) 15 cm + 30 cm = 45 cm
300 = 6,67
45
Considerando 7, o custo será de 7 x R$ 90,00 = R$ 630,00.
- V) 15 cm + 40 cm = 55 cm
300 = 5,45
55
Considerando 6, o custo será de 6 x R$ 120,00 = R$ 720,00.
Portanto, o menor orçamento será o da loja III.
Alternativa: C
QUESTÃO 174
O arquiteto Renzo Piano exibiu a maquete da nova sede do Museu Whitney de Arte Americana, um prédio assimétrico que tem um vão aberto para a galeria principal, cuja medida da área é 1672 space straight m squared.
Considere que a escala da maquete exibida é 1 : 200.
Época, n. 682, jun. 2011 (adaptado).
A medida da área do vão aberto nessa maquete, em centímetro quadrado, é
(A) 4,18.
(B) 8,36.
(C) 41,80.
(D) 83,60.
(E) 418,00.
Resolução:
Área do vão aberto: 1672 m2
Escala linear: 1 : 200
Escala = Tamanho maquete: Tamanho real
Escala superfície: (1:200)2
Logo:
(1/200)2 = x/1672 =
1/40 000 = x/1671
x = 0,0418 m2
Convertendo em cm2 temos:
x = 0,0418 m2 . 104 = 418 cm2
Alternativa: E
QUESTÃO 175
O gráfico apresenta o valor total de exportações e o valor total de importações, ao longo de um período, em bilhão de dólares. O saldo da balança comercial brasileira é dado pelo valor total de exportações menos o valor total de importações num mesmo período.
Fonte: Ministério do Desenvolvimento. Disponível em: http://blogs.estadao.com.br. Acesso em: 20 fev. 2013 (adaptado).
Considere que os saldos da balança comercial brasileira, nos três meses destacados no gráfico, sejam representados por:
S1: saldo em junho de 2009;
S2: saldo em janeiro de 2010;
S3: saldo em junho de 2010.
A ordenação dos saldos S1, S2 e S3 do maior para o menor, é
(A) S1, S2 e S3
(B) S2, S1 e S3
(C) S2, S3 e S1
(D) S3 S1 e S2
(E) S, 3S1 e S1
Resolução:
Analisando o gráfico, tem-se:
S1 = 14,5 -10 = 4,5 bilhões de dólares
S2 = bilhão de dólares
S3 = 17,1 – 14,8 = 3,2 bilhão de dólares
Logo:
S1 > S3 > S2
Alternativa: A
QUESTÃO 176
Um instituto de pesquisa constatou que, nos últimos dez anos, o crescimento populacional de uma cidade foi de 135,25%.
Qual é a representação decimal da taxa percentual desse crescimento populacional?
(A) 13 525,0
(B) 135,25
(C) 13,525
(D) 1,3525
(E) 0,13525
Resolução:
Crescimento populacional: 135,25%.
135,25 = 135,25 = 1,3525
100
Logo, sua representação decimal será dada por:
Alternativa: D
QUESTÃO 177
Um fazendeiro pretende construir um galinheiro ocupando uma região plana de formato retangular, com lados de comprimentos L metro e C metro. Os lados serão cercados por telas de tipos diferentes. Nos lados de comprimento L metro, será utilizada uma tela cujo metro linear custa R$ 20,00, enquanto, nos outros dois lados, uma que custa R$ 15,00. O fazendeiro quer gastar, no máximo, R$ 6 000,00 na compra de toda a tela necessária para o galinheiro, e deseja que o galinheiro tenha a maior área possível.
Qual será a medida, em metro, do maior lado do galinheiro?
(A) 85
(B) 100
(C) 175
(D) 200
(E) 350
Resolução:
O retângulo tem lados L e C, portanto a relação entre o valor total gasto e as dimensões é:
2L . (R$ 20,00) + 2C . (R$ 15,00 = R$ 6 000,00
4L + 3C = 600
C = 600 – 4L
3
C = 200 – 4L
3
Área do galinheiro:
A = L . C(200 – 4L
3
Desse modo, a área do galinheiro, em função da dimensão L, é dada por uma função do segundo grau com concavidade para baixo e com raízes:
200 – 4 L = 0
3
L = 150
O valor máximo da função é atingido no vértice da parábola quando
L = 0 + 150 = 75 m
2
Assim, para L = 75 m, como
C = 200 – 4 L
3
C = 200 – 4 . 75 = 200 – 100 =
3
C = 100 m
Alternativa: B
QUESTÃO 188
Uma professora de matemática utiliza em suas aulas uma "máquina caça-números" para verificar os conhecimentos de seus estudantes sobre representações de números racionais. Essa máquina tem um visor dividido em seis compartimentos e, na lateral, uma alavanca. Cada estudante puxa a alavanca e espera que os compartimentos parem de girar. A partir daí, precisa responder para a professora em quais posições se encontram os números que representam a mesma quantidade.
Um estudante puxou a alavanca, aguardou que os compartimentos parassem de girar e observou os números apresentados no visor.
A configuração da máquina naquele instante está apresentada na imagem.
Esse estudante respondeu corretamente à pergunta da professora. As posições indicadas pelo estudante foram
(A) I, II e IV.
(B) II, IV e V.
(C) II, III e V.
(D) III, V e VI.
(E) III, IV e VI
Resolução:
Os números representados no visor podem ser simplificados da seguinte maneira:
(A) I.
41/2 = √4 = 2
(B) II. 4 . 1 = 4 + 1 = 4,5
2 2
(C) III. 10 = 2 = 0,222...
45 9
(D) IV. 4,5
(E) V. 4 = 0,8
5
Alternativa: B
QUESTÃO 189
Uma caneca com água fervendo é retirada de um forno de micro-ondas. A tempertura T, em grau Celsius, da caneca, em função do tempo t, em minuto, pode ser modelada pela função T = (t) = a + 80bt, representada no gráfico a seguir.
Os valores das constantes a e b são
(A) a = 20; b = log(0,5)
(B) a = 100; b = 0,5
(C) a = 20; b = (0,5)1/10
(D) a = 20; b = (40)1/10
80
(E) a = 20; b = 40
Resolução:
Do gráfico:
T(0) = a + 80 . b0 = 100
a + 80 = 100
a = 100 – 80
a = 20
T(20) a + 80 . b20 = 40
a + 80 . b20 = 40
20 + 80 . b20 = 40
80 . b20 = 20
b20 = 1 = (0,5)2
4
b = (0,5)2/20
b = (0,5)1/10
Assim, a = 20 e b = (0,5)1/10
Alternativa: C
QUESTÃO 180
Em uma empresa é comercializado um produto em embalagens em formato de cilindro circular reto, com raio medindo 3 cm, e altura medindo 15 cm. Essa empresa planeja comercializar o mesmo produto em embalagens em formato de cubo, com capacidade igual a 80% da capacidade da embalagem cilíndrica utilizada atualmente. se 3 como valor aproximado para π = 3.
A medida da aresta da nova embalagem, em centímetro, deve ser
(A) 6
(B) 18
(C) 6√6
(D) 6
(E) 6
Resolução:
Volume da embalagem cilíndrica:
V =πr2h
V =π(3)2 . 15
V = 135π cm3
Com π = 3, do enunciado:
V = 135 . 3 = 405 cm3
Volume da embalagem cúbica:
V = a3 = 0,8 . 4.5 = 324 = 27 . 12
a =
a = 3
Alternativa: E
